TUTORIEL | Machine Learning : comment mettre en place l’apprentissage d’un réseau de neurones ?

Nous allons aborder aujourd’hui l’apprentissage d’un réseau de neurones. Cet article fait suite à notre précédent tutoriel « Comprendre ce qu’est un réseau de neurones et en créer un ! ». Vous découvrirez ici comment apprend un réseau de neurones et surtout comment vous allez pouvoir, concrètement, mettre en place cet apprentissage.

Notre réseau de neurones

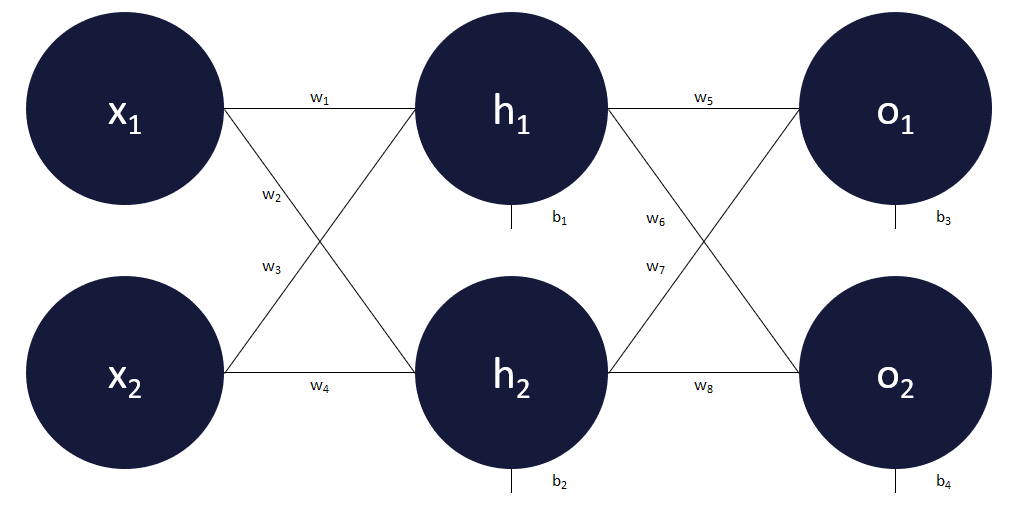
Voici le réseau de neurones que nous allons utiliser dans cet article afin de vous expliquer comment un réseau de neurones apprend par lui-même à corriger ses erreurs.

Ce réseau est donc composé :

• d’une couche d’entrée qui comprend 2 entrées x₁ et x₂,
• d’une couche cachée qui comprend 2 neurones h₁ et h₂,
• d’une couche de sortie qui comprend également 2 neurones o₁ et o₂, ces 2 sorties seront respectivement désignées comme o_1prédit et o_2prédit,
• il y a 8 poids et 4 biais.

La fonction d’activation choisie est la fonction sigmoïde.

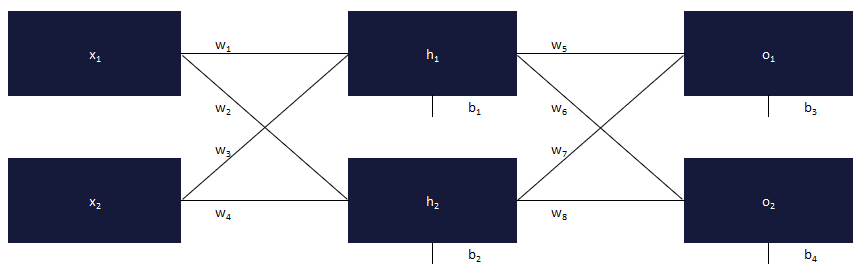
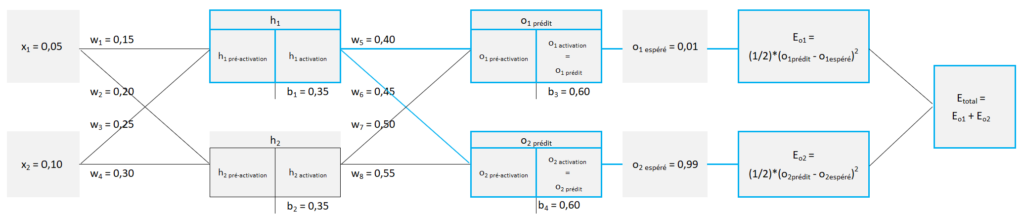
Pour des raisons pratiques, et comme j’utilise Excel afin d’illustrer mes propos, notre réseau devient le suivant (rien n’a changé, hormis la mise en page).

Nos données d’entrées et nos sorties attendues

  Ce que nous souhaitons faire avec ce réseau :

Quelles que soient les valeurs x₁ et x₂ renseignées en entrée, nous souhaitons que o₁ soit le plus proche possible de 0,01 et o₂ le plus proche possible de 0,99.

Rem. cet objectif n’a aucun intérêt dans un environnement de production, il est simplement utilisé ici pour des raisons pédagogiques.

Nous allons utiliser, pour la phase d’apprentissage, des valeurs fixes pour x₁ et x₂ (respectivement 0,05 et 0,10). Puis, nous changerons ces valeurs après la phase d’apprentissage afin de voir si les sorties prédites restent respectivement proches de 0,01 et de 0,99.

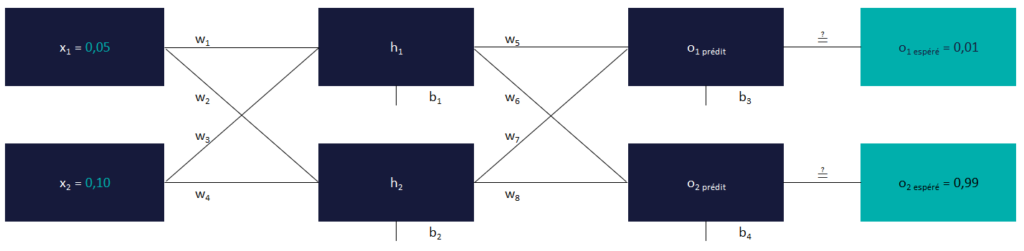
Nos poids et biais aléatoires

Nous allons commencer avec des poids et biais aléatoires, ce sont ces valeurs que la machine va faire évoluer, seule, afin que x₁ et x₂ soient, respectivement, e plus proche de 0,01 et 0,99, et ce, indépendamment de leur valeur.

Notre réseau, dans son état initial, est donc le suivant (cliquer sur le schéma pour l’agrandir).

  Comme vous pouvez le voir, 3 éléments ont été ajoutés :

• E_o1 >>> l’erreur o₁ représente la moitié de la différence, au carré, entre o_1prédit et o_1espéré (ex. o_1prédit = 0,5 ; o_1espéré = 0,01 ; E_o1 = (1/2) * (0,5 – 0,01)² = 0,12005)
• E_o2 >>> l’erreur o₂ représente la moitié de la différence, au carré, entre o_2prédit et o_2espéré (ex. o_2prédit = 0,3 ; o_1espéré = 0,99 ; E_o2 = (1/2) * (0,3 – 0,99)² = 0,23805)
• E_total >>> l’erreur totale est tout simplement la somme de E_o1 et de E_o2.

Dans la mesure où nos 2 dernières couches (couche cachée et couches de sortie) comprennent une formule de pré-activation et une formule d’activation, notre réseau se présente sous la forme suivante (cliquer sur le schéma pour l’agrandir).

Pour rappel, si l’on prend h₁, il est calculé en 2 temps :

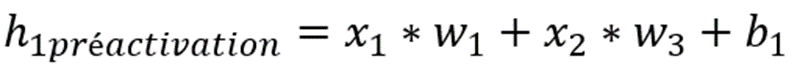
C’est la même chose pour h₂, o₁, o₂.

1ère itération

En faisant les calculs, voici les résultats obtenus (cliquer sur le tableau pour l’agrandir).

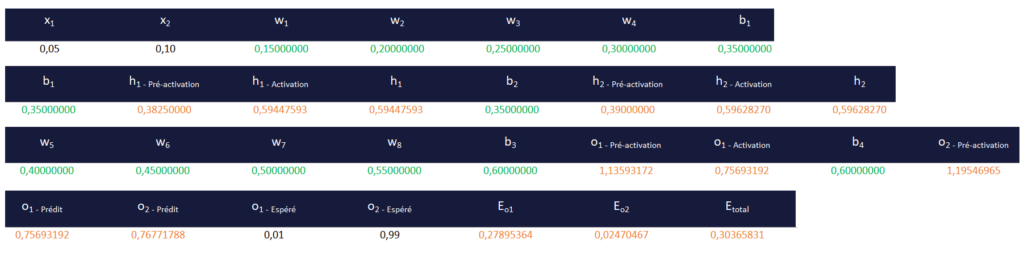
• En noir : des données fixes, qui ne changeront pas entre 2 itérations,
• En vert : les poids et biais qui vont être optimisés à chacune des itérations, et donc être modifiés
• En orange : les résultats des formules de pré-activation et d’activation qui seront calculés à chaque itération en fonction des nouveaux poids et biais modifiés à chaque itération

h_{1préactivation} par exemple, est égal à :

x₁ * w₁ + x₂ * w₃ + b₁ = 0,05 * 0,15 + 0,10 * 0,25 + 0,35 = 0,3825

h_1activation, est donc égal à :

1 / (1 + e^-0,3825) = 0,594475931

L’action consistant à faire les calculs de la gauche vers la droite, au regard des poids et biais à un instant T, est appelée forward.

Descente de gradient

Pour rappel, nous souhaitons trouver des poids et biais qui permettent, quelles que soient les entrées x₁ et x₂, d’avoir un o_1prédit le plus proche de 0,01 et o_2prédit le plus proche de 0,99.

Comme pour les régressions linéaires simple et multiple, nous allons utiliser la méthode de la descente de gradient, appelée rétropropagation du gradient dans un réseau de neurones.

Notre fonction coût E_total dépend des valeurs de :
– w₁
– w₂
– w₃
– w₄
– w₅
– w₆
– w₇
– w₈
– b₁
– b₂
– b₃
– b₄

Ce sont les seules valeurs qui peuvent être modifiées dans ce réseau de neurones.

Nous allons chercher les 12 dérivées partielles de E_total par rapport à chacune de ces variables, puis utiliser ces dérivées pour calculer leurs nouvelles valeurs.

Pour rappel et par exemple pour b₄ :

Si vous ne comprenez pas l’intérêt d’utiliser les dérivées afin d’optimiser ces 12 valeurs, nous vous invitons à consulter notre article sur la régression linéaire et la descente de gradient.

Pour calculer ces dérivées, nous allons partir de la couche de sortie puis revenir vers la couche d’entrée en calculant, pour chacune des couches, les dérivées de chacun des poids et biais la constituant.

Dérivée de E_total par rapport à w₅

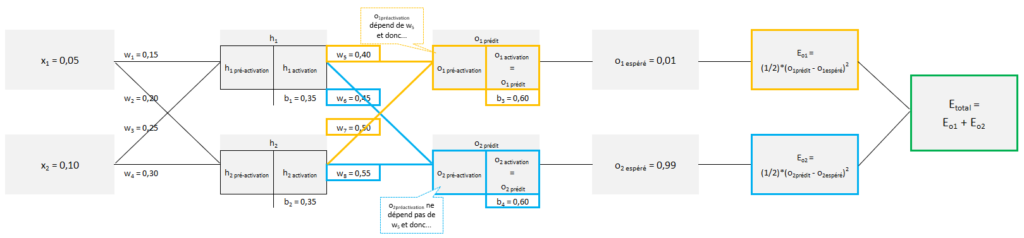
  Avant de rentrer dans les calculs, nous allons décomposer E_total.

  E_total est la somme de E_o1 et de E_o2.

  Prenons E_o1.

  Les éléments qui permettent de calculer E_o1 sont indiqués en orange ci-dessus.

  Effectivement,

• E_o1 dépend de o_1prédit,
• o_1prédit (qui est égal à o_1activation) dépend de o_{1préactivation}
• o_{1préactivaion} dépend de b₃, w₅ et de w₇.

Pour rappel, nous souhaitons dériver E_total par rapport à w₅. Si l’on prend le « chemin » de E_o1, on voit bien que E_o1 dépend de w5. La dérivée de E_o1 par rapport à w₅ n’est pas nulle.

Prenons maintenant E_o2.

Les éléments qui permettent de calculer E_o2 sont indiqués en bleu ci-dessus.

Effectivement,

• E_o2 dépend de o_2prédit,
• O_2prédit (qui est égal à o_2activation) dépend de o_{2préactivation}
• O_{2préactivaion} dépend de b₄, w₆ et de w₈.

Pour rappel, nous souhaitons dériver E_total par rapport à w₅. Si l’on prend le chemin de E_o2, on voit, à la différence de E_o1, que E_o2 ne dépend pas de w₅. La dérivée de E_o2 par rapport à w₅ est nulle.

Revenons à nos calculs, si on développe notre formule, voici ce que cela donne.

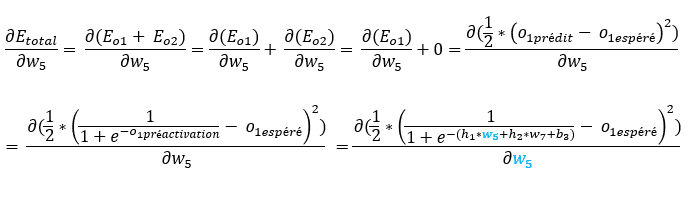
Rappelez-vous…

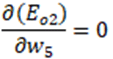
Cela semble compliqué sauf si on utilise le « théorème de dérivation des fonctions composées ».

Celui-ci indique que :

  – si nous avons une fonction : f(g(h(x)))

  – alors sa dérivée partielle est :

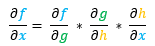
Dans notre situation :

f = E_o1
x = w₅
g = o_1activation
h = o_{1préactivation}

Effectivement,

• f (E_o1) dépend de g (o_1activation),
• g (o_1activation) dépend de h (o_{1préactivation}).

Ainsi :

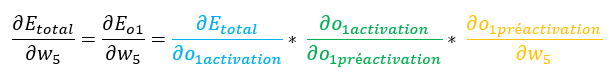
On va traiter ces éléments un par un.

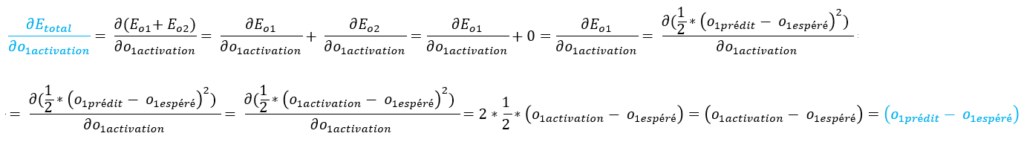
Explications :
– la dérivée de E_o2 par rapport à o_1activation est égale à 0 car E_o2 ne dépend pas de o_1activation.
– o_1activation = o_1prédit

Explications :
– la dérivée d’une sigmoïde est égale à : (sigmoïde * (1 – sigmoïde))

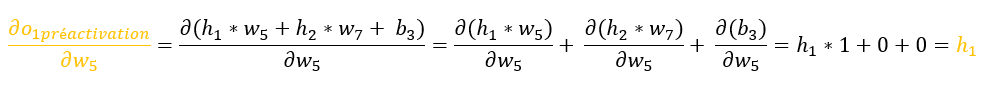
Revenons donc à :

Dérivée de E_total par rapport à w₆

Le raisonnement est identique, je vais simplement indiquer en bleu les éléments qui ont changé par rapport à la dérivée de E_total par rapport à w₅.

Dérivée de « E_total » par rapport à « w₆« 

= (o_2prédit – o_2espéré) * (o_2prédit * (1 – o_2prédit)) * h₁

Dérivée de E_total par rapport à w₇

Dérivée de « E_total » par rapport à « w₇« 

= (o_1prédit – o_1espéré) * (o_1prédit * (1 – o_1prédit)) * h₂

Dérivée de E_total par rapport à w₈

Dérivée de « E_total » par rapport à « w₈« 

= (o_2prédit – o_2espéré) * (o_2prédit * (1 – o_2prédit)) * h₂

Dérivée de E_total par rapport à b₃

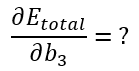
Comme ci-dessus, si l’on remplace les éléments par leur calcul, voici, de manière littéraire, ce que cela donne.

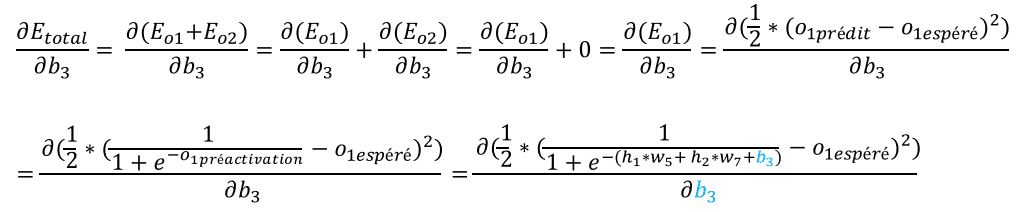
Explications :
– la dérivée de E_o2 par rapport à b₃ est nulle car E_o2 ne dépend pas de b₃.

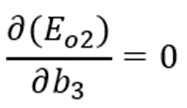
Comme précédemment, nous allons utiliser le « théorème de dérivation des fonctions composées ».

Ainsi :

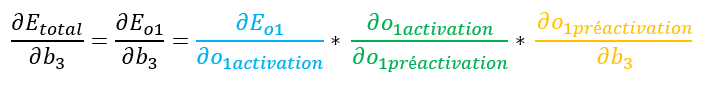
Comme précédemment, on va traiter ces éléments un par un.

Notre équation complète est donc :

Dérivée de E_total par rapport à b₄

Le raisonnement étant identique, j’indique en bleu les éléments qui changent.

Dérivée de « E_total » par rapport à « b₄« 

= (o_2prédit – o_2espéré) * (o_2prédit * (1 – o_2prédit))

Dérivée de E_total par rapport à w₁

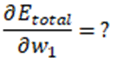
En raison du théorème de dérivation des fonctions composées…

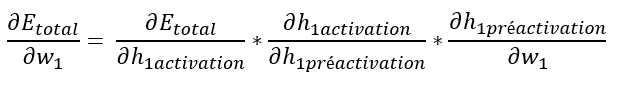
Intéressons-nous tout d’abord à :

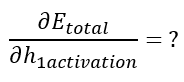
Si l’on regarde notre réseau de neurones, on voit que h_1activation influence o₁ (et donc E_o1) mais aussi o₂ (et donc E_o2).

On peut donc écrire :

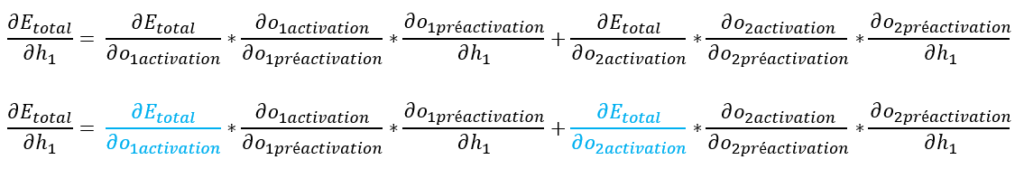
Nous allons nous intéresser aux dérivées de E_total par rapport respectivement à o_1activation et à o_2activation.

Commençons par ∂E_total / ∂o_1activation.

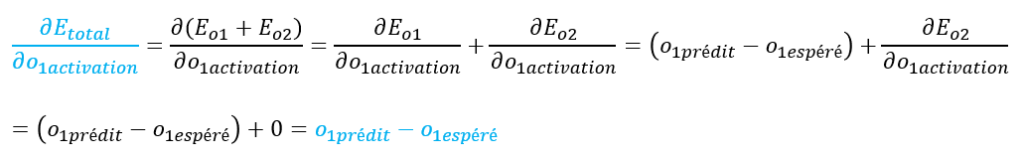
Explications :
– la dérivée de E_o1 par rapport à o_1activation a déjà été calculée précédemment
– la dérivée de E_o2 par rapport à o_1activation est égale à 0 car E_o2 ne dépend pas de o_1activation
– o_1activation = o_1prédit

Et maintenant, ∂E_total / ∂o_2activation.

Explications :
– la dérivée de E_o1 par rapport à o_2activation est égale à 0 car E_o1 ne dépend pas de o_2activation
– la dérivée de E_o2 par rapport à o_2activation a déjà été calculée précédemment
– o_2activation = o_2prédit

Notre formule ∂E_total / ∂h₁ devient :

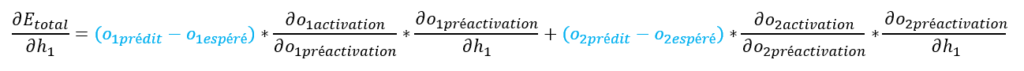
Les éléments en noir ont déjà été calculés précédemment, notre formule finale E_total / ∂h₁ devient :

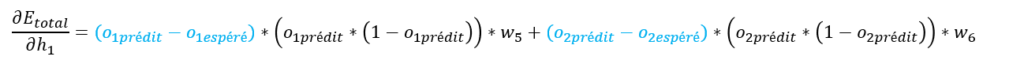
Revenons à l’objectif de cette partie, à savoir le calcul de ∂E_total / ∂w₁.

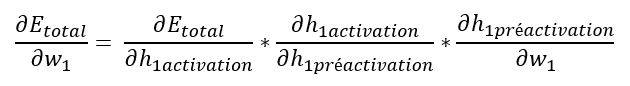
Nous venons de calculer ∂E_total / ∂h₁ (rappel, h₁ = h_1activation), il nous reste à calculer les 2 autres éléments de notre formule (en jaune et violet ci-dessous).

Notre équation complète est donc :

Dérivée de E_total par rapport à w₂

Dérivée de « E_total » par rapport à « w₂« 

= [ ((o_1prédit – o_1espéré)*(o_1prédit)*(1-o_1prédit)*w₇) + ((o_2prédit – o_2espéré)*(o_2prédit)*(1-o_2prédit)*w₈) ] * [ ((h₂)*(1-h₂)) ] * [ x₁ ]

Dérivée de E_total par rapport à w₃

Dérivée de « E_total » par rapport à « w₃« 

= [ ((o_1prédit – o_1espéré)*(o_1prédit)*(1-o_1prédit)*w₅) + ((o_2prédit – o_2espéré)*(o_2prédit)*(1-o_2prédit)*w₆) ] * [ ((h₁)*(1-h₁)) ] * [ x₂ ]

Dérivée de E_total par rapport à w₄

Dérivée de « E_total » par rapport à « w₄« 

= [ ((o_1prédit – o_1espéré)*(o_1prédit)*(1-o_1prédit)*w₇) + ((o_2prédit – o_2espéré)*(o_2prédit)*(1-o_2prédit)*w₈) ] * [ ((h₂)*(1-h₂)) ] * [ x₂ ]

Dérivée de E_total par rapport à b₁

Dérivée de « E_total » par rapport à « b₁« 

= [ ((o_1prédit – o_1espéré)*(o_1prédit)*(1-o_1prédit)*w₅) + ((o_2prédit – o_2espéré)*(o_2prédit)*(1-o_2prédit)*w₆) ] * [ ((h₁)*(1-h₁)) ]

Dérivée de E_total par rapport à b₂

Dérivée de « E_total » par rapport à « b₂« 

= [ ((o_1prédit – o_1espéré)*(o_1prédit)*(1-o_1prédit)*w₇) + ((o_2prédit – o_2espéré)*(o_2prédit)*(1-o_2prédit)*w₈) ] * [ ((h₂)*(1-h₂)) ]

Forward et Backward

L’activité consistant à faire les calculs de la gauche vers la droite, c’est-à-dire de la couche d’entrée vers la couche de sortie, est appelé Forward.

A la fin de celle-ci, une erreur est calculée. Dans notre cas, il s’agit de E_total.

Cette erreur va nous permettre de faire une marche arrière, et de corriger légèrement – et à chaque itération – nos poids et biais.

Nous allons donc faire des itérations successives afin que les dérivées partielles de E_total par rapport à tous les poids et biais soient le plus proche possible de 0.

Concrètement, voici les étapes que nous allons suivre :

• Etape initiale : cette étape initiale a déjà été faite car elle consiste à donner des valeurs aléatoires aux poids et biais. Cette étape n’est à faire qu’une seule fois.
• Etape 1 : calcul de toutes les dérivées partielles de tous les poids (w) et biais (b) par rapport à E_total, et ce au regard de toutes les valeurs à un instant T du réseau,
• Etape 2 : si celles-ci ne tendent pas vers 0, les variables associées peuvent encore être optimisées selon la descente de gradient. De nouveaux poids (w) et biais (b) seront calculés en même temps, de la même manière que dans le cas de la régression linéaire, à savoir : nouveau wⁱ = ancien wⁱ – learning rate * ∂Etotal/∂w (rem. c’est la même chose pour les biais).
• Etape 3 : les nouveaux poids (w) et biais (b) calculés seront utilisés dans le cadre d’une nouvelle itération, et permettront de recalculer tout ce qui en dépend, à savoir : h_{1préactivation}, h_1activation, h_{2préactivation}, h_2activation, o_{1préactivation}, o_1activation, E_o1, o_{2préactivation}, o_2activation, E_o2, E_total

On recommence les étapes 1, 2, 3 un très grand nombre de fois jusqu’à trouver :

E_o1 très proche de 0
E_o2 très proche de 0

et par voie de conséquence

o_1prédit très proche de 0,01
o_2prédit très proche de 0,99

Si l’on change les valeurs de x₁ et de x₂, on trouvera toujours en sortie E_o1 et E_o2 très proche de 0… et donc… et donc o_1prédit très proche de 0,01, o_2prédit très proche de 0,99.

Vous pouvez trouver un fichier excel ici qui je l’espère vous aidera à lever vos interrogations éventuelles. Celui-ci vous décrira à nouveau notre réseau de neurones, ce que l’on en attend, son fonctionnement, mais surtout les calculs.