TUTORIEL | Machine Learning : comprendre ce qu’est un réseau de neurones et en créer un !

Dans ce nouvel article, nous allons voir ce qu’est un réseau de neurones en Machine Learning, à quoi il sert, comment il fonctionne et enfin comment il apprend. Comme pour notre précédent article, destiné à vous apprendre comment développer votre première régression linéaire avec la descente de gradient, vous n’avez pas besoin de solides connaissances en mathématiques pour comprendre les concepts qui vont être présentés. C’est parti !

Contextes

Un réseau de neurones peut résoudre de très nombreux problèmes liés à la Data. Avant de vous expliquer ce qu’est un réseau de neurones exactement, appréhendons ce concept à travers 3 exemples.

1. La reconnaissance d’images

Cette image représente-t-elle un chien ou un chat ?

2. Le dosage de médicaments

Quelle(s) dose(s) d’un médicament (ou de médicaments) faut-il administrer à un patient afin de le guérir ?

3. L’identification d’un attribut au regard d’autres attributs

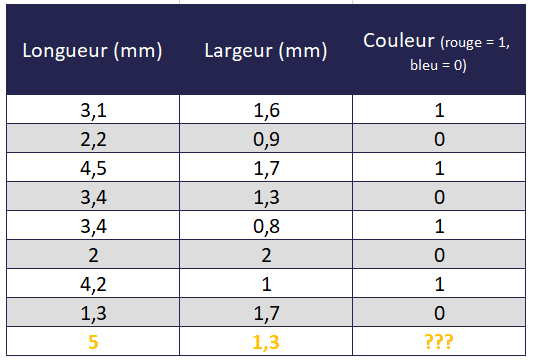
Quelle est la couleur de la dernière fleur au regard de sa longueur et de sa largeur ?

Qu’est-ce qu’un réseau de neurones ?

C’est un ensemble de « neurones artificiels » organisés de la manière suivante. Nous verrons par la suite ce qu’est un « neurone artificiel ».

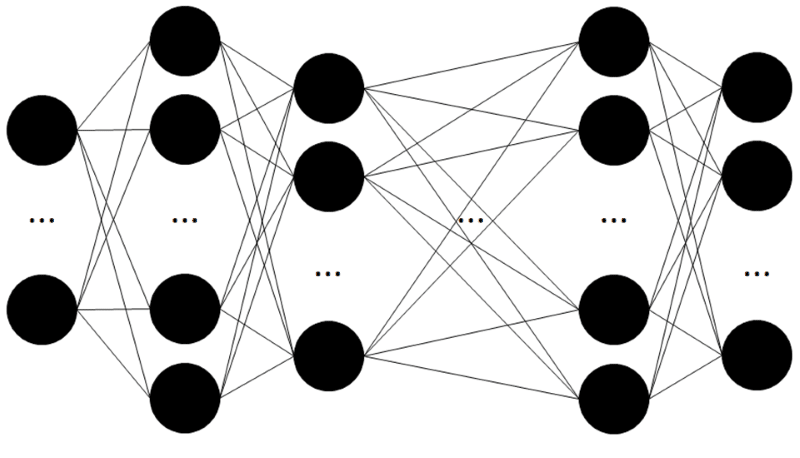
  Il y a différentes couches.

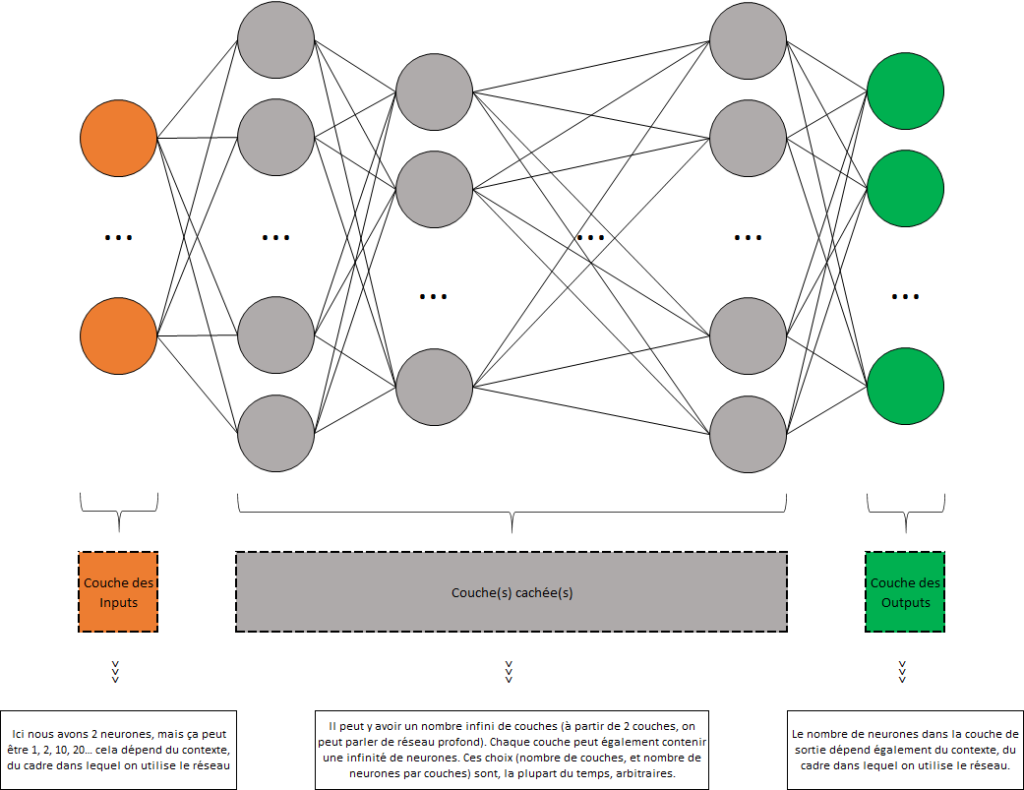
Chaque « couche » est connectée, reliée à l’ensemble des neurones de la couche précédente.

A quoi sert un réseau de neurones ?

Un réseau sert, dans la majorité des cas, à trouver n’importe quelle fonction, relation entre de « 1 à n variables prédites » et de « 1 à n variables explicatives ».

Reprenons les 3 contextes indiqués précédemment.

1er contexte : la reconnaissance d’images

Quelle est la relation entre les pixels d’une image et ce qu’elle représente ?

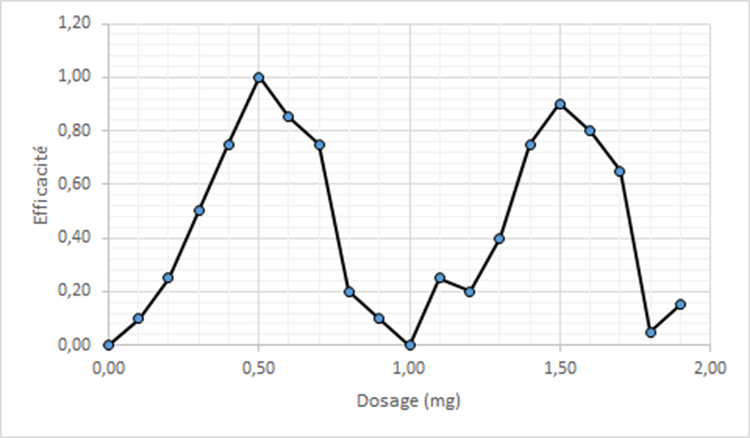
2^ème contexte : le niveau d’efficacité d’un dosage de médicament

Quelle est la relation entre le dosage d’un médicament et son efficacité ?

3^ème contexte : la couleur d’une fleur

Quelle est la relation entre le duo « largeur, longueur » d’une fleur et sa couleur ?

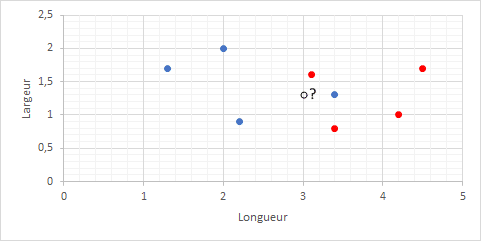
Détails des couches

Couche de l’input (des inputs)

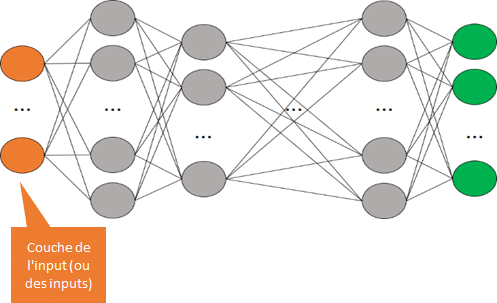
Le contenu de cette couche varie en fonction du contexte, du cas d’usage concerné par le réseau de neurones. Voici quelques exemples au regard de nos cas d’usage précédemment présentés. Dans tous les cas, ce ne sont pas des neurones artificiels que l’on trouve en entrée mais des inputs.

1er contexte : la reconnaissance d’images

1.1. L’image en couleur

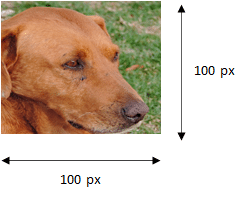
Cette image a une taille de 100 px sur 100 px. Un pixel contient 3 valeurs (R, G, B). Cette image est donc composée de 100 x 100 x 3 = 30 000 valeurs. Ces 30 000 valeurs vont représenter notre input layer (couche d’entrée). Il y a aura donc 30 000 neurones dans la première couche. Nous parlerons dans un prochain article du réseau neuronal convolutif (CNN), qui modifie la façon d’appréhender la valeur des couches en entrée d’un NN (Neural Network).

  1.2. L’image en noir et blanc

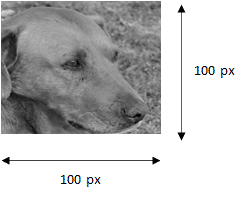
Cette image a une taille de 100 px sur 100 px. Un pixel contient 1 valeur comprise entre 0 et 1 (0 = blanc, 1 = noir, gris = 0,5…). Cette image est donc composée de 100 x 100 = 10 000 valeurs. Ces 10 000 valeurs vont représenter notre input layer (couche d’entrée). Il y aura donc 10 000 neurones dans la première couche.                                                                                               

2^ème contexte : le niveau d’efficacité d’un dosage de médicament

Dans cette situation, notre réseau n’aurait qu’un seul input dans sa couche d’entrée (le dosage en mg du médicament).

3^ème contexte : la couleur d’une fleur

Dans cette situation, notre réseau aurait en entrée 2 inputs (1° input = longueur, 2° input = largeur).

Couche(s) cachée(s)

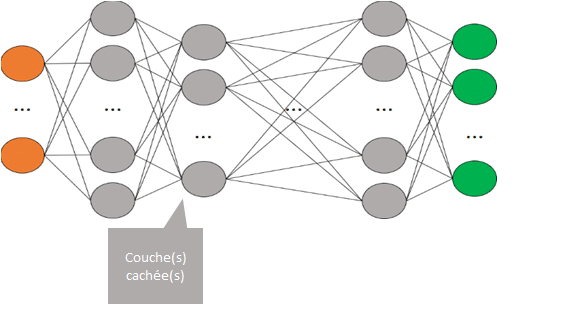
Cette fois, chaque « rond » représente bien un neurone artificiel.

Comme indiqué précédemment, le nombre de couches est variable et variera en fonction du contexte mais aussi de la puissance de calcul disponible pour entraîner et utiliser le réseau. C’est la même chose pour le nombre de neurones par couches.

1. Tous les neurones de la (ou des) couche(s) cachée(s) se décomposent comme suit.

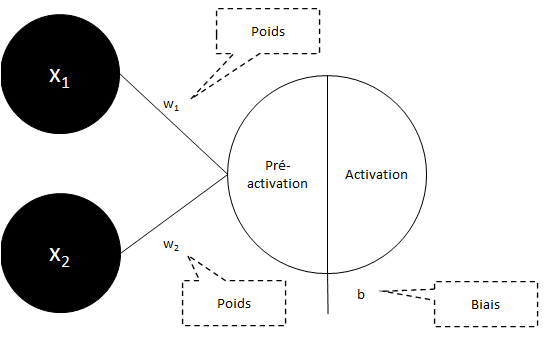
Un neurone est composé de 2 fonctions, la pré-activation et l’activation.

2. La formule de pré-activation est toujours la même.

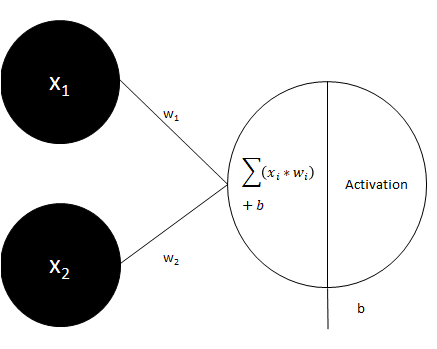
Cette formule multiplie tout simplement tous les x avec les w, additionne les résultats obtenus, puis ajoute un biais.

Exemple :

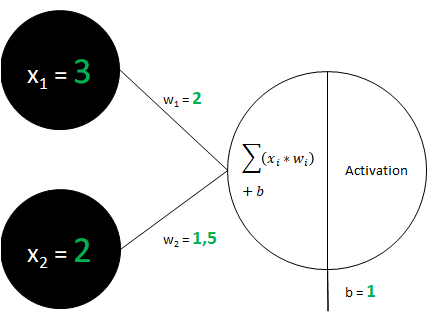
Dans la situation décrite dans l’image, notre pré-activation est égale à :

= x₁ * w₁ + x₂ * w₂ + b
= 3×2 + 2×1,5 + 1
= 10

D’autres exemples :

3. Passons désormais à la formule d’activation, celle-ci change en fonction du contexte, du cas d’usage concerné par le réseau. Voici les principales formules d’activation utilisées.

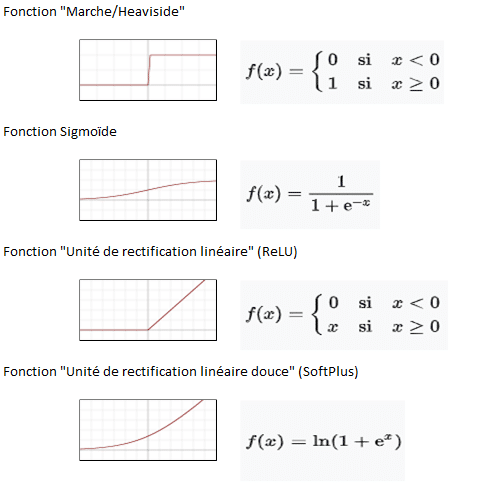
4. Pour l’exemple, nous allons utiliser la fonction sigmoïde.

Précédemment, nous avions calculé la pré-activation (x₁ * w₁ + x₂ * w₂ + b = 3*2 + 2*1,5 + 1 = 10). Nous allons appliquer la fonction sigmoïde à ce résultat (nous allons remplacer notre « x » par « le résultat de la pré-activation »).

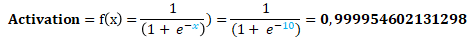
Notre neurone devient :

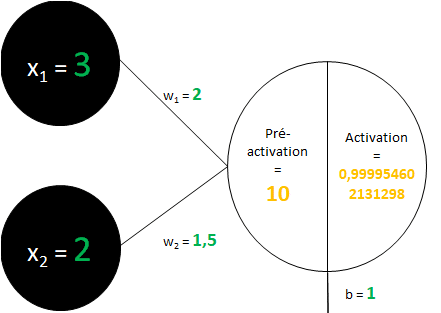
5. D’autres exemples

Couche de l’output (des outputs)

1. Le nombre de neurones dans cette couche est variable et correspond au contexte du réseau.

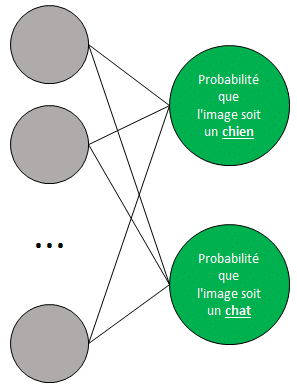
1^er contexte : la reconnaissance d’images

Pour rappel, on souhaite connaître le pourcentage que l’image représente un chat, et le pourcentage que l’image représente un chien.

Nous aurons donc 2 neurones.

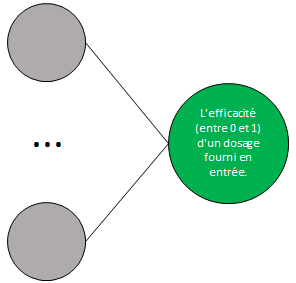
2^ème contexte : le niveau d’efficacité d’un médicament en fonction de son dosage

Dans cette situation, il n’y aurait qu’un seul neurone dans la couche de sortie.

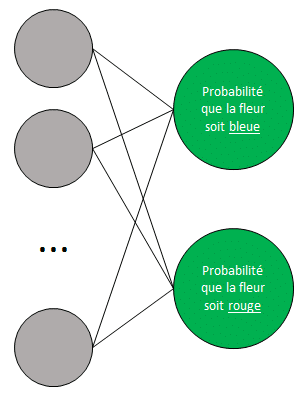
3^ème contexte : la couleur d’une fleur en fonction de sa hauteur et de sa largeur

Dans cette situation, il y aurait 2 neurones dans la couche de sortie.

2. Quel que soit le nombre de neurones dans cette couche de sortie(s), les neurones fonctionnent comme ceux des couches cachées à la seule différence qu’il y a des contextes où seule la fonction de pré-activation est utilisée, et d’autres (c’est majoritairement le cas), où les 2 fonctions sont utilisées (pré-activation et activation).

L’entraînement

L’entraînement d’un réseau de neurones consiste à faire en sorte que la machine trouve, seule :

• les bonnes valeurs pour tous les biais (b) du réseau
• les bonnes valeurs pour tous les poids (w) du réseau

Concrètement, nous allons donc, dans l’ordre :

1. Fournir des données aléatoires pour tous les b et w du réseau,
2. Fournir en entrée (dans la couche d’entrée) des données labellisées (i.e. des données dont on connaît la sortie attendue – ex. on sait que cette image fournie en entrée représente un chien, on attend que le réseau prédise qu’il s’agit d’un chien, on sait que cette fleur est bleue, on attend que le réseau nous réponde que la fleur est bleue…),
3. Laisser la machine faire ses calculs (i.e. calculer les résultats des neurones (pré-activation et activation) jusqu’à la couche de sortie),
4. Laisser la machine comparer les résultats obtenus avec les résultats attendus,
5. Laisser la machine corriger plus ou moins fortement les b et w afin de minimiser l’erreur (l’écart entre ce qui a été prédit et ce que l’on espérait voir être prédit),
6. Recommencer (i.e. fournir en entrée des données labellisées, laisser la machine faire ses calculs jusqu’à la couche de sortie, calculer l’erreur… etc.)

Vous avez maintenant vu ce qu’est un réseau de neurones, à quoi il peut servir. Dans notre prochain article, nous verrons comment le faire apprendre, c’est-à-dire comment faire en sorte qu’il trouve par lui-même les valeurs les plus optimales pour tous les poids et biais.

👉 Retrouvez toute notre actu en temps réel en nous suivant sur LinkedIn 👈