TUTORIEL | Machine Learning : développez votre première régression linéaire avec la descente de gradient

Comment une machine peut-elle apprendre ? Telle est l’une des questions à laquelle nous allons répondre dans cette série d’articles. Vous découvrirez ainsi les principaux algorithmes utilisés en Machine Learning, et ce de manière extrêmement didactique. Pas besoin d’avoir fait un doctorat en informatique et/ou mathématiques pour comprendre leur fonctionnement. Après avoir parcouru ces algorithmes, vous comprendrez mieux comment fonctionne le machine learning, et surtout ce qu’il peut vous apporter.

Dans cet article, vous allez découvrir l’algorithme le plus simple du Machine Learning : la régression linéaire. Nous en profiterons pour vous expliquer une notion légèrement plus complexe mais surtout utilisée par de nombreux autres algorithmes : la descente de gradient.

Comprendre la notion de Machine Learning

Imaginons que nous nous situons dans une forêt composée uniquement d’arbres de la même espèce, tous sont exposés de la même manière aux éléments, tous ont une composition minérale et organique du sol identique…

Bref, ils sont tous identiques à l’exception de leur âge. Certains sont jeunes (le tronc a donc un petit rayon, leur taille est petite également) et d’autres plus âgés (tronc avec un large rayon, grande taille).

Les données disponibles

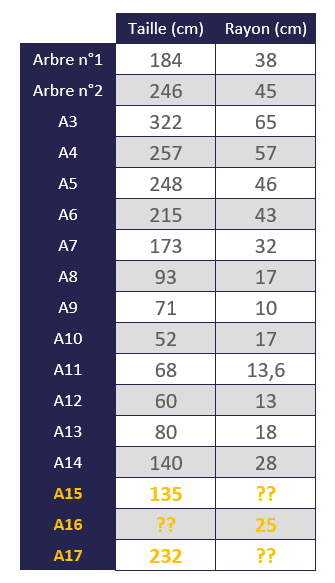
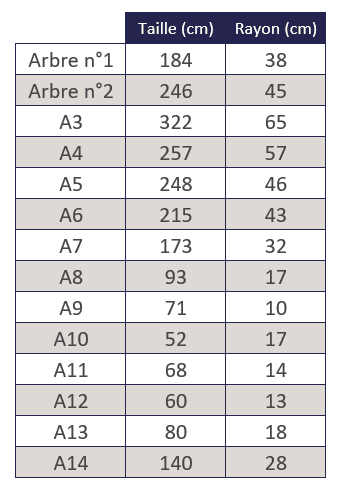
Nous avons 14 arbres dans cette forêt et avons mesuré pour chacun d’entre eux la taille et le rayon (en cm), puis avons reporté ces résultats dans le tableau suivant.

Nous souhaitons ainsi connaître le rayon d’un 15ème arbre dont on connaît la taille (135 cm), et nous souhaitons également connaître la taille d’un 16ème arbre dont on connaît le rayon (25 cm)…

Intérêt

Nous reportons ces mesures dans un graphique et obtenons le nuage de points suivant. Ce sont les valeurs observées.

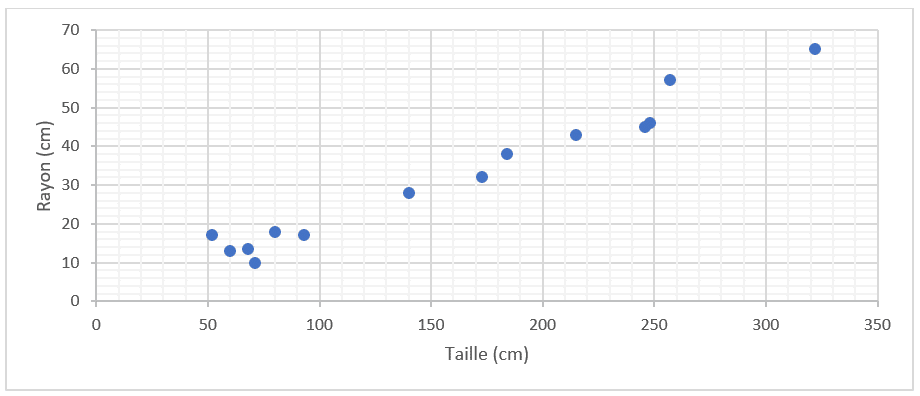
L’être humain y voit tout de suite une relation entre la taille et le rayon. Il pourrait donc facilement dessiner une droite qui relierait au mieux tous ces points.

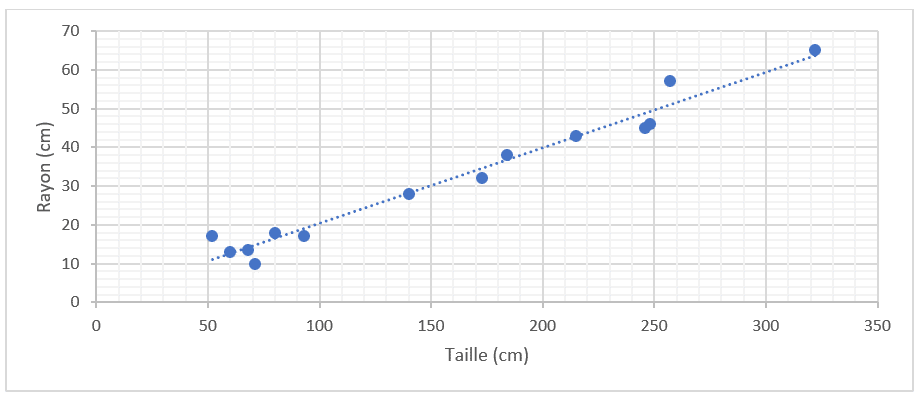
Avec cette droite, nous pourrions connaître le rayon d’un nouvel arbre en mesurant sa taille (et inversement), et ainsi remplir le tableau suivant. On parle ici de valeurs prédites.

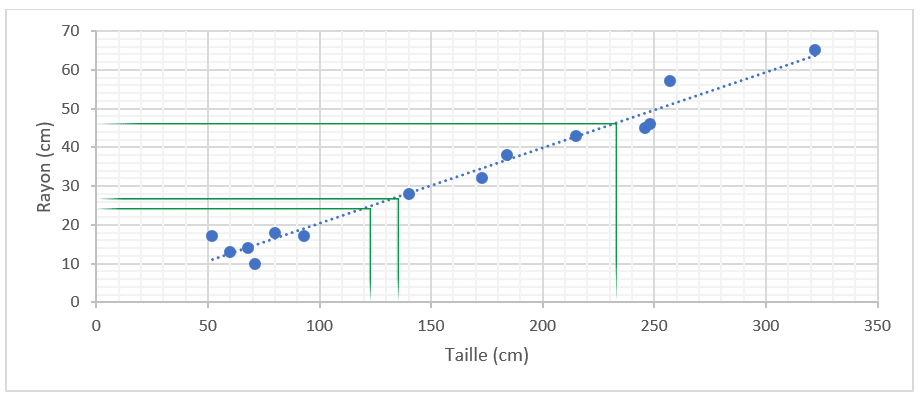
Nous allons maintenant voir comment la machine « trouve » cette droite qui relie la taille d’un arbre à son rayon.

Les explications

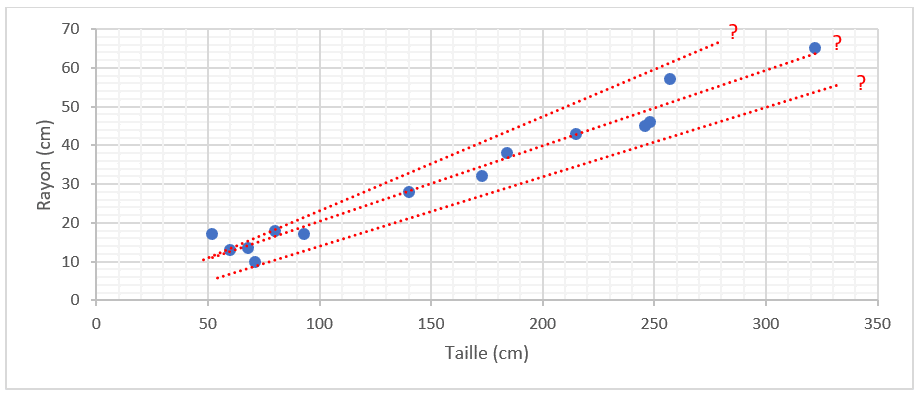
La première chose à comprendre est qu’il existe une infinité de droites possibles, mais laquelle est la meilleure ?

En réalité, c’est très simple, la meilleure droite est celle qui minimise les écarts entre la réalité (les tailles et rayons réellement observés) et les prédictions (les tailles et rayons calculés).

Pour le comprendre, rappelez-vous vos cours de mathématiques, une droite proposant une relation entre 2 variables x et y a pour fonction :

f(x) = a*x + b

a représente la pente, b l’intersection.

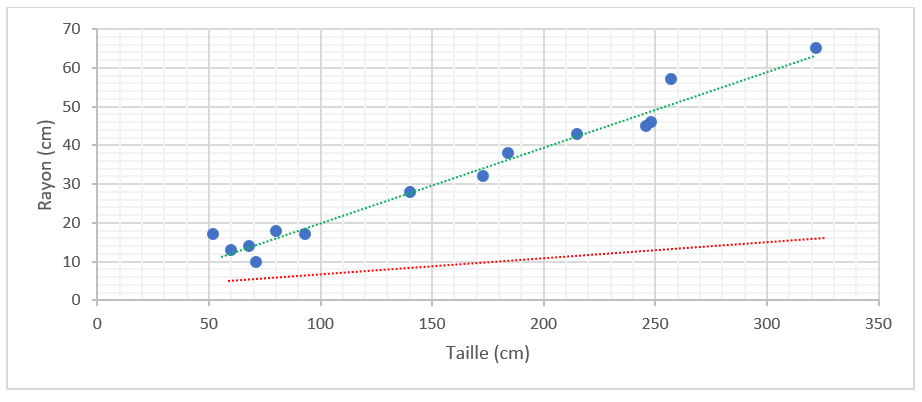
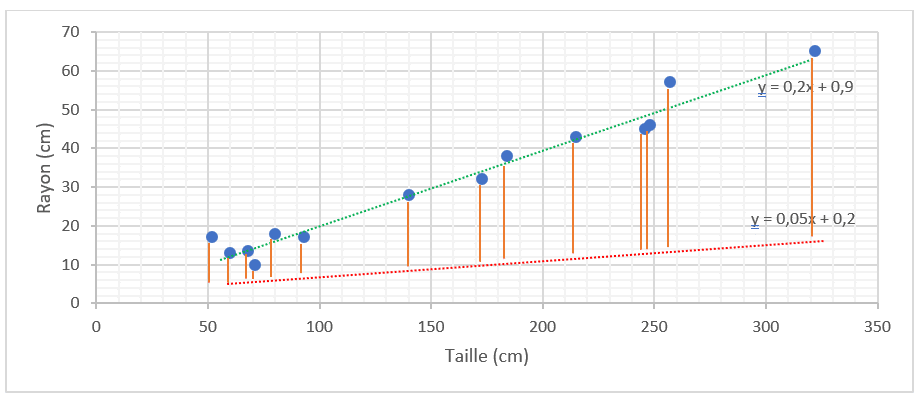
La droite rouge est moins bonne que la droite verte, car elle présente des écarts plus importants que l’autre droite.

On va calculer les différences entre la réalité (valeurs observées) et la prédiction (valeurs calculées par les droites).

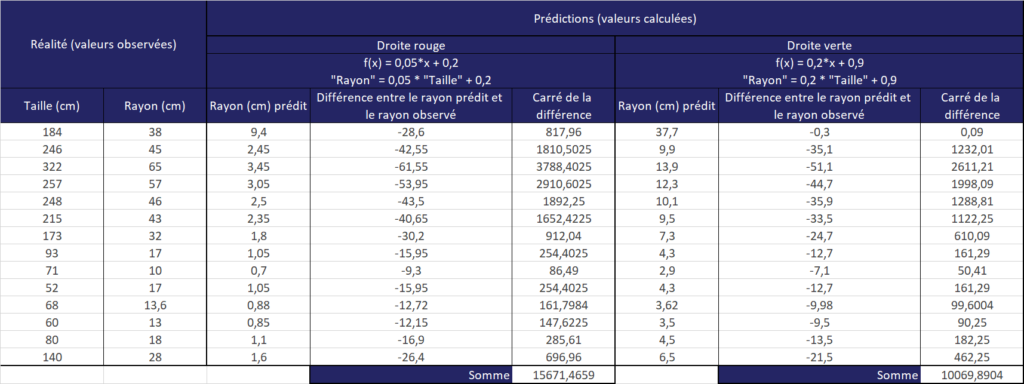
Afin de ne pas annuler les différences, appelées aussi écarts (en additionnant par exemple une différence positive avec une différence négative), nous avons pris le carré de l’écart, puis avons additionné tous ces carrés.

La droite verte présente la somme des carrés des écarts la plus petite (10 069 < 15 671), elle est donc meilleure que la droite rouge.

Pour cet exemple très simple, nous avons comparé 2 droites que nous avons choisies, mais en réalité il y a une infinité de droites. Comment la machine peut-elle trouver la meilleure droite parmi cette infinité de droites, c’est-à-dire celle dont la somme des carrés des écarts à la moyenne est la plus faible ? Il existe pour cela différents moyens.

Moyen 1 : Tester toutes les valeurs possibles pour a et b

Cette méthode n’est pas du tout recommandée (et surtout impossible à utiliser telle quelle dans un véritable environnement), mais elle va nous permettre d’illustrer certains points que l’on utilisera dans la suite de cet article.

En prenant des valeurs aléatoires pour a et b (pour rappel, la fonction est f(x) = a*x + b), on obtient les résultats suivants.

Avec cette méthode, la somme des écarts au carré la plus petite est égale à 144,51. Cela correspond à « a= 0,19 ; b = 1 ».

La droite ressemble à celle-ci. Elle semble effectivement passer au plus proche des points.

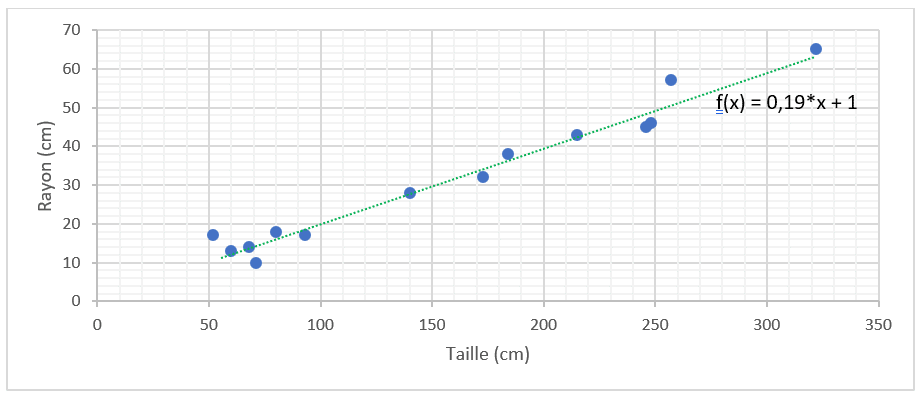
Pourtant, nous sommes loin d’avoir testé toutes les valeurs de a et de b (ex. la droite ne serait-elle pas meilleure par exemple avec a = 0,195 et b = 1,002 ?), nous ne sommes donc pas sûr qu’il n’existe pas une meilleure droite. C’est pour cela qu’il existe la descente de gradient.

Moyen 2 : Utiliser la descente de gradient aléatoire.

Pour rappel, nous souhaitons que la somme des carrés des erreurs soit la plus petite possible.

Pour continuer l’explication, nous allons non pas prendre la somme mais la moyenne. Cette moyenne est appelée fonction coût.

Elle s’écrit de la manière suivante :

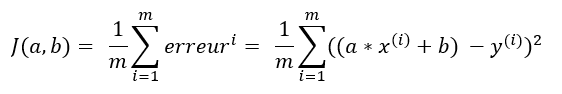
m = représente le nombre d’observations, dans notre exemple, le nombre d’arbres, à savoir 14 arbres.

(rem. la littérature divise la fonction coût par 2m et non par m, je choisis ici de diviser par m pour ne pas compliquer l’explication).

Avec nos données d’exemple, qui pour rappel, sont les suivantes, nous aurions la fonction coût suivante :

J(a, b) =
          (1/14) *
          [
            (a*184+b-38)^2
            + (a*246+b-45)^2
            + (a*322+b-65)^2
            + (a*257+b-57)^2
            + (a*248+b-46)^2
            + (a*215+b-43)^2
            + (a*173+b-32)^2
            + (a*93+b-17)^2
            + (a*71+b-10)^2
            + (a*52+b-17)^2
            + (a*68+b-13,60)^2
            + (a*60+b-13)^2
            + (a*80+b-18)^2
            + (a*140+b-28)^2
          ]

Ce que l’on souhaite découvrir, c’est le minimum de cette fonction coût, i.e. les valeurs de a et de b permettant de minimiser la fonction coût.

Dans un premier temps, on va simplifier la fonction afin de mieux comprendre la descente de gradient.

La fonction n’est plus « f(x) = a*x + b » mais « f(x) = a*x » (cela signifie que la droite passera obligatoirement par le point {y ; x = 0 ; 0}).

La fonction coût devient alors :

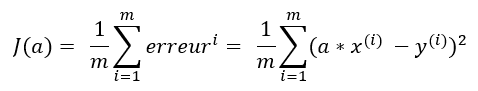
Avec nos données d’exemple, cette fonction coût est la suivante :

J(a) 

= (1/14)*((a*184-38)^2+(a*246-45)^2+(a*322-65)^2+(a*257-57)^2+ (a*248-46)^2+(a*215-43)^2+(a*173-32)^2+(a*93-17)^2+(a*71-10)^2+ (a*52-17)^2+(a*68-13,60)^2+(a*60-13)^2+(a*80-18)^2+(a*140-28)^2)

= (452 381/14)*a^2 – 12867,114*a + 1290,854

En remplaçant a par quelques valeurs aléatoires, on obtient le tableau suivant.

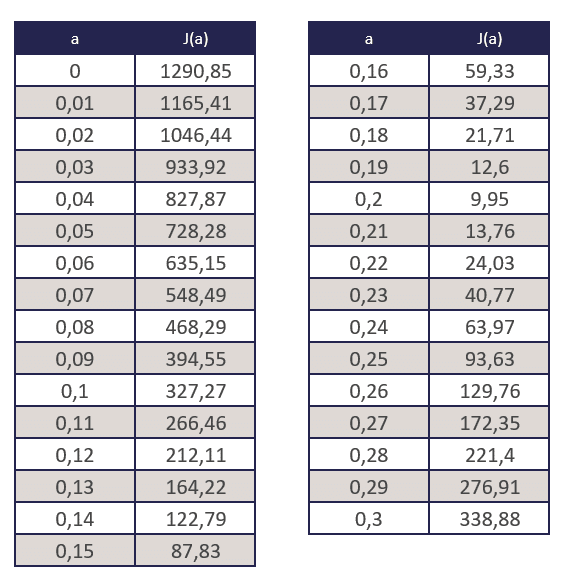
Si l’on affiche ces chiffres sur un nuage de points et en dessinant une courbe, nous obtenons le graphique suivant.

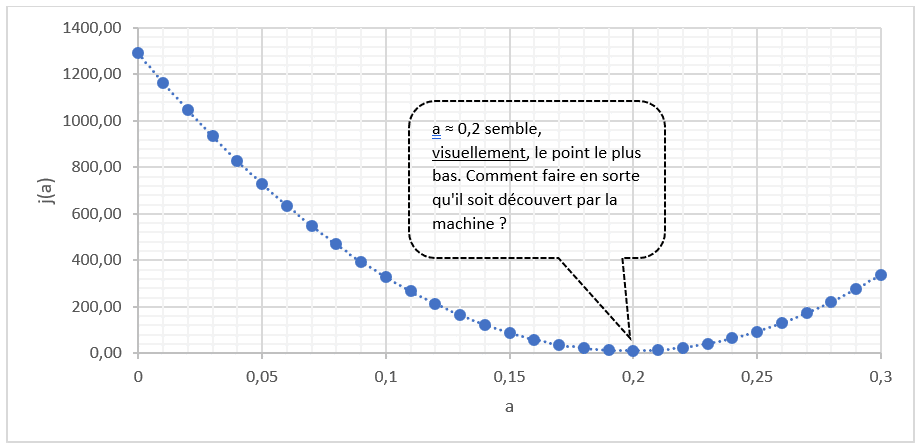
Visuellement, l’être humain peut trouver la valeur de a qui minimise la fonction coût J(a), dans notre exemple, ça semble être a = 0,2. Mais comment la machine peut-elle trouver cette valeur, et surtout comment peut-elle la trouver de manière plus précise que l’être humain (après tout, visuellement, ça semble être 0,20 mais n’est-ce pas plutôt 0.199, 0.201, 0.20001… etc. ?) ?

Pour cela, on va utiliser la dérivée. Pour rappel, la dérivée mesure la pente d’un point située sur une courbe.

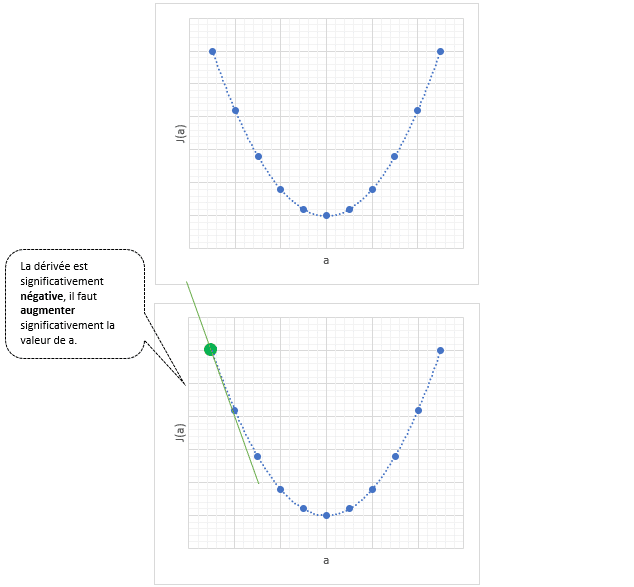
La descente de gradient aléatoire est une suite d’opérations que voici.

Etape a. La machine choisit aléatoirement un nombre pour a.

  Exemple : a = -758

Etape b. La machine calcule la dérivée afin de savoir si elle est à gauche ou à droite du point minimum.

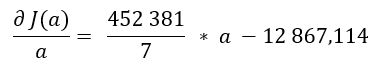
La dérivée de « a = -758 » est négative, cela signifie que la pente descend, on se situe à gauche du minimum.

On peut donc continuer et proposer un « a » plus grand que « -758 ».

Étape c. La machine propose aléatoirement un nouveau chiffre plus grand que « -758 ».

Exemple : a = -432

Étape d. La machine calcule la dérivée afin de savoir si elle est à gauche ou à droite du point minimum.

La dérivée de « a = -432 » est toujours négative, cela signifie que la pente descend, on se situe à gauche du minimum.

On peut donc continuer et proposer un a plus grand que « -432 ».

Étape e. La machine propose aléatoirement un nouveau chiffre plus grand que « -432 ».

Exemple : a = 23

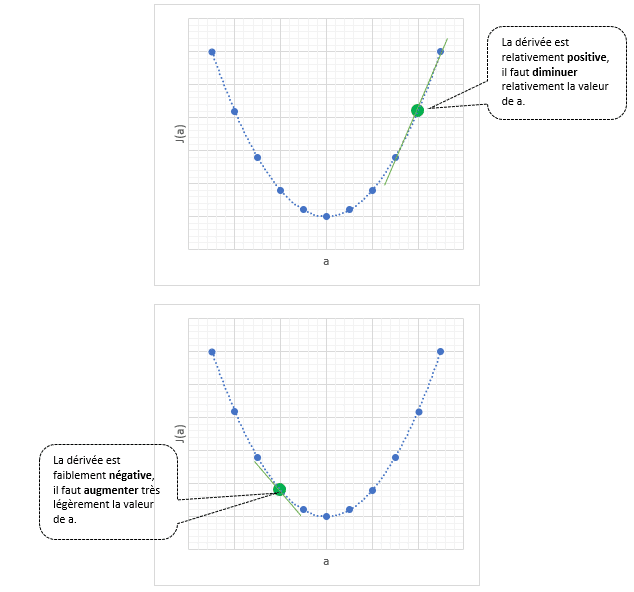
Étape f. La machine calcule la dérivée afin de savoir si elle est à gauche ou à droite du point minimum.

La dérivée de « a = 23 » est positive, cela signifie que la pente monte, on se situe à droite du minimum.

On peut donc continuer et proposer un a situé entre « -432 » et « 23 ».

Etape … n. La machine se stabilise et trouve la valeur de a permettant de minimiser la fonction de coût.

Cette méthode fonctionne mais peut prendre beaucoup de temps et nécessite de nombreux calculs, on va donc voir comment gagner du temps et minimiser le nombre de calculs à effectuer.

Moyen 3 : Utiliser la descente de gradient « optimisée »

Plutôt que proposer aléatoirement à chacune des étapes une nouvelle valeur pour a, on va soustraire à a un certain pourcentage de la dérivée calculée à l’étape précédente, pourcentage que l’on appelle « learning rate ». Cette technique est appelée communément la descente de gradient. Rassurez-vous, avec quelques exemples, ça vous semblera bien plus facile.

Etape a. Comme précédemment, la machine choisit aléatoirement un nombre pour a, c’est la seule étape ou un chiffre aléatoire va être utilisé.

Exemple : a = -758

Etape b. Comme précédemment, la machine calcule la dérivée afin de voir si celle-ci est extrêmement proche de 0 ou non.

a = -758
Dérivée de J(a) par rapport à a = (452381 / 7) * a – 12 867,114 = (452381 / 7) * (-758) – 12 867,114 = – 48999266,83

La dérivée n’est pas du tout proche de 0, une nouvelle valeur de a doit être trouvée.

Etape c. La nouvelle valeur de a est calculée de la manière suivante :

« Nouveau a » = « Ancien a » – « learning_rate » * « Dérivée »

Pour cet article, le « learning_rate » (taux d’apprentissage) sera égal à 0,00001 (en règle générale, il est égal à 0,01 et son identification fait l’objet de méthodes spécifiques que nous n’aborderons pas dans cet article). Quoi qu’il en soit, il sera pour cet article constant et égal à 0,00001.

Cela donne donc :
« Nouveau a » = -758 – (0,00001 * -48999266,83) = -268,0073317

Etape d., e. … n. La machine recommence indéfiniment jusqu’à ce :
– la « dérivée de J(a) par rapport à a » soit très proche de 0 (tende vers 0)
– la valeur de a se stabilise (ne change presque plus entre chaque itération)

Sous forme de tableaux, voici ce que cela donne.

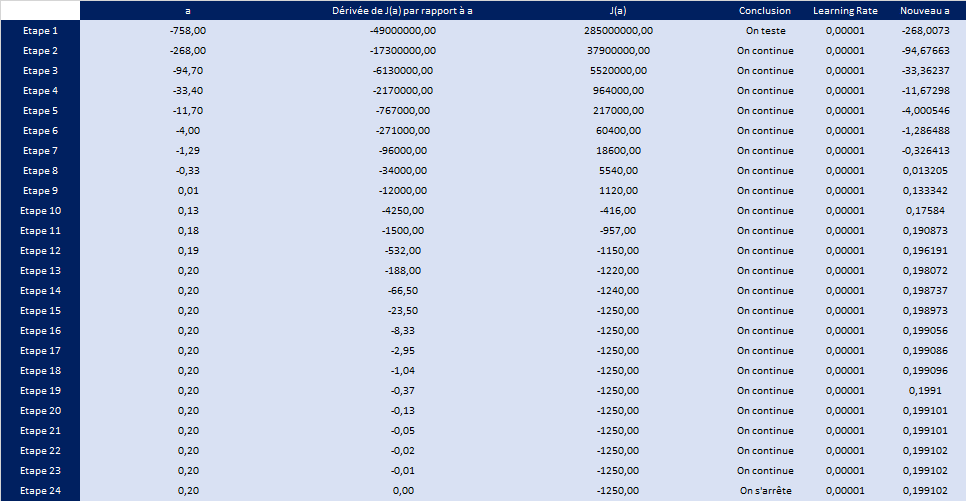
Au bout de la 24° étape, la valeur de a se stabilise et est égale à 0,199102.

Moyen 4 : Utiliser la descente de gradient « optimisée » pour trouver, cette fois, a et b

Nous allons enfin voir dans cette dernière partie comment utiliser la descente de gradient optimisée à la fois à a et à b.

Le fonctionnement est à peu près identique.

Afin de simplifier les calculs, nous allons prendre les valeurs suivantes.

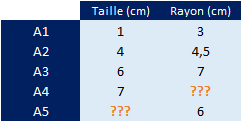
L’objectif reste identique, trouver le rayon d’un arbre dont la taille est de 7 cm et la taille d’un arbre dont le rayon est de 6 cm.

Il faut seulement comprendre que l’ajout d’une nouvelle variable, en l’occurrence b, transforme notre fonction coût en un graphique en 3D dimensions.

En 3 dimensions, une fonction coût pourrait se présenter sous cette forme.

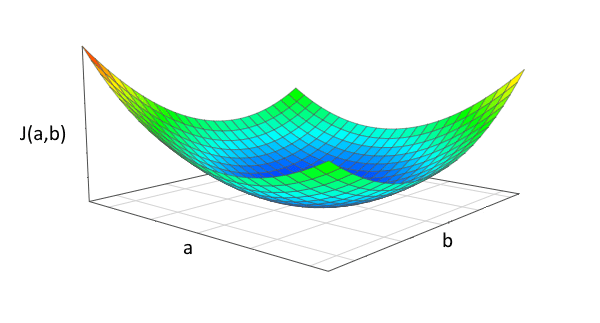
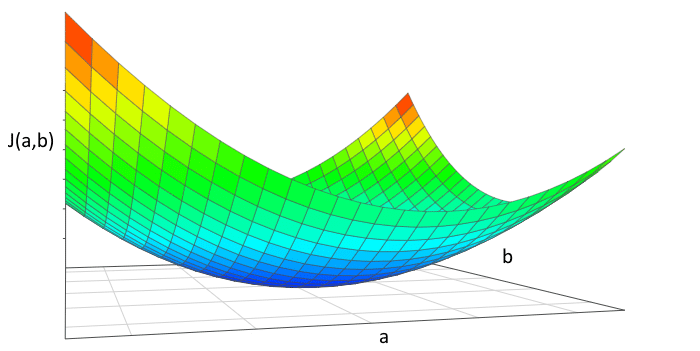
L’objectif reste donc le même, quelles sont les valeurs respectives de a et de b permettant de minimiser la fonction coût.

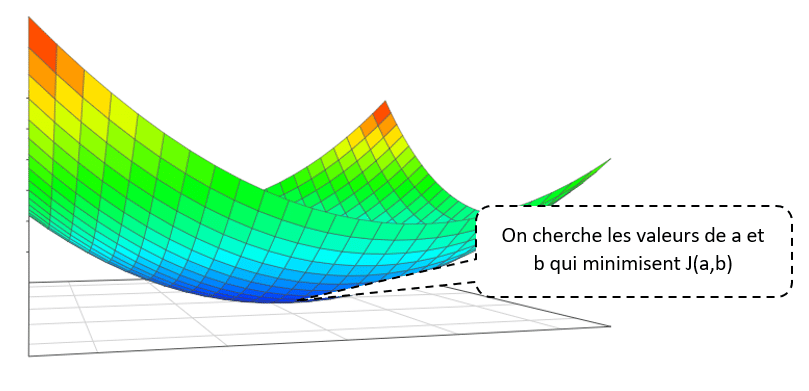
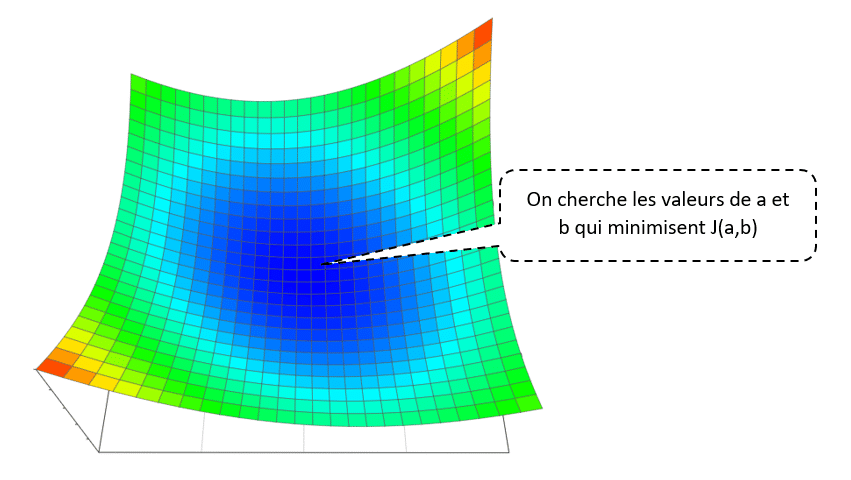
Pour cela, on va une nouvelle fois utiliser la descente de gradient optimisée.

Voici la fonction coût après introduction de la variable b.

J(a,b) = (3 – (a*1+b))^2 + (4,5 – (a*4+b))^2 +  (7 – (a*6+b))^2

Cette fois, nous allons calculer deux dérivées :

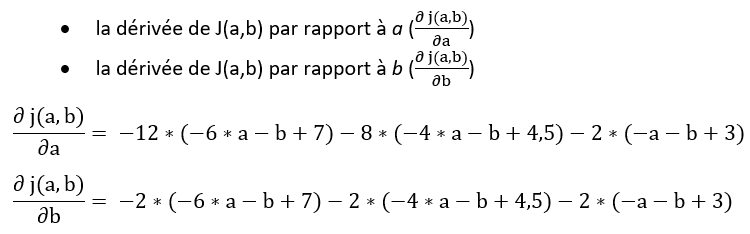
Comme précédemment, nous allons procéder par une succession d’étapes itératives jusqu’à ce que les valeurs de a et b se stabilisent. Des valeurs de a et de b stabilisées signifieraient :

• des dérivées très proches de 0 (i.e. horizontales)

Etape c.

On analyse les résultats et on prend une décision.

Les 2 dérivées ne sont pas du tout proches de 0, on continue donc.

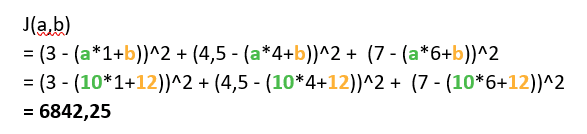
Etape d.

Comme précédemment, on va utiliser un learning rate afin de calculer les 2 nouvelles valeurs de a et de b.

Learning rate = 0,001

  “Nouveau a”
  = “Ancien a” – “Learning rate” * “Dérivée de J(a,b) par rapport à a”
  = 10 – 0,001 * 1198
  = 8,802

  “Nouveau b”
  = “Ancien b” – “Learning rate” * “Dérivée de J(a,b) par rapport à b”
  = 12 – 0,001 * 263
  = 11,737

Etape e.

On recommence.

La machine calcule les dérivées de J(a,b) par rapport à a et à b

Etape f.

On analyse les résultats et on prend une décision.

Les 2 dérivées ne sont pas du tout proches de 0, on continue donc.

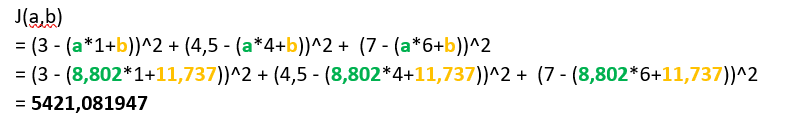
Etape … n :

On recommence jusqu’à ce que les valeurs de a et de b se stabilisent.

Sous forme de tableaux, voici les résultats obtenus à chacune des étapes.

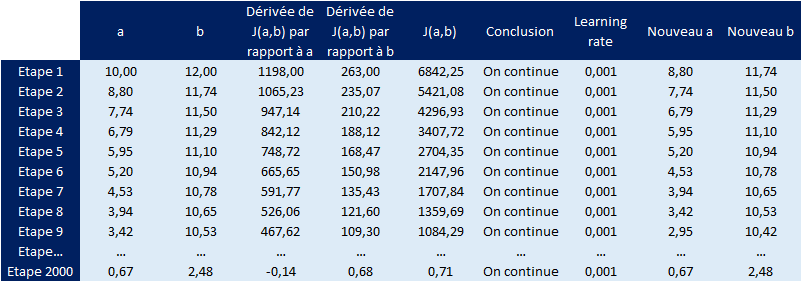
On voit qu’à partir de la 2000° étape, les valeurs se sont bien stabilisées.
  a ≃ 0,6724…
  b ≃ 2,4812… 

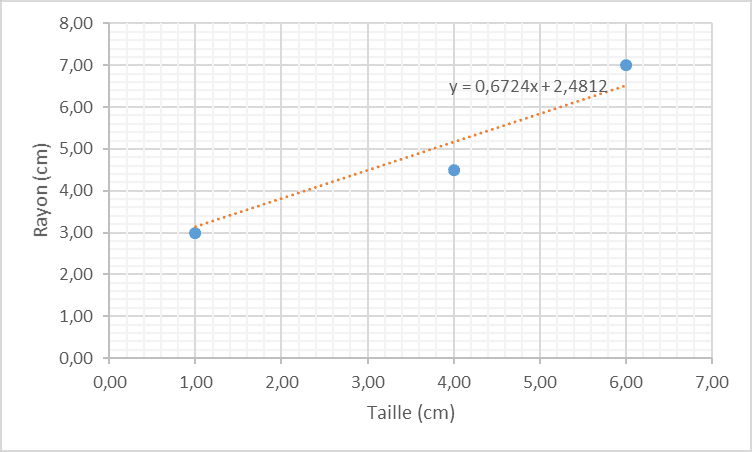
Notre relation entre taille et rayon est donc la suivante :

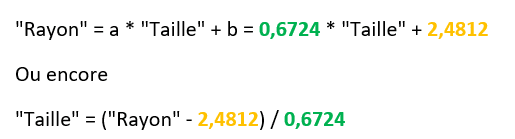
 Nous pouvons ainsi calculer les valeurs manquantes.

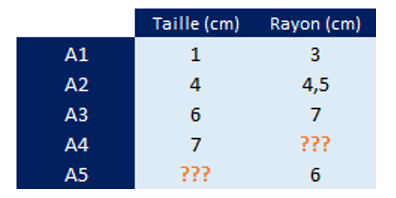
  Le rayon de l’arbre A4

  = 0,6724 * 7 + 2,4812
  = 7,188

  La taille de l’arbre A5

  = (6 – 2,4812) / 0,6724
  = 5,233

Et voilà ! Vous venez de découvrir la descente de gradient optimisée appliquée à une régression linéaire simple (i.e. f(x) = a*x + b). Dans de prochains articles, nous décortiquerons d’autres algorithmes…