TUTORIEL | Deep Learning : le Réseau neuronal convolutif (CNN)

Nous vous avons expliqué dans notre précédents articles la descente de gradient et son utilisation dans la régression linéaire, le fonctionnement et l’intérêt d’un réseau de neurones, mais aussi son apprentissage, nous allons voir cette fois un réseau de neurones particulier appelé le réseau neuronal convolutif ou « réseau neuronal à convolution » (CNN – Convolution Neural Network). Ce type d’algorithme est particulièrement utilisé afin de classifier des images.

Le réseau neuronal convolutif est un type d’algorithme particulièrement utilisé afin de classifier des images, par exemple :

Actions utilisées dans un CNN

Un CNN applique généralement 3 types d’opérations différentes à une image afin d’en extraire les informations pertinentes.

Ces 3 types d’opérations sont les suivantes :

• La convolution
• Le pooling
• La fonction d’activation de type ReLU

 Nous allons nous intéresser à chacune de ses opérations.

La convolution

Avant d’expliquer en détails ce qu’est une convolution, nous allons comparer ces 2 images.

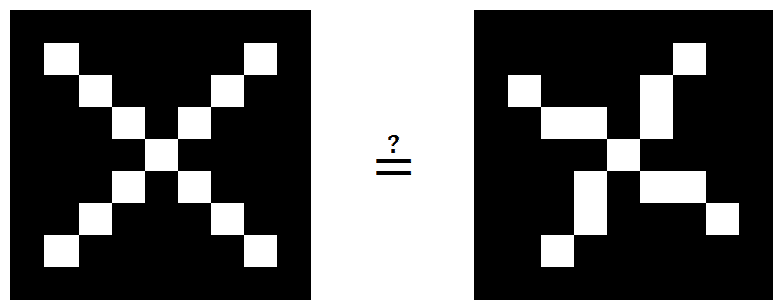
Ces 2 images sont constituées de 81 pixels (9×9). En codant la couleur des pixels par une valeur entre -1 (pixel noir) et +1 (pixel blanc), nous obtenons les images suivantes.

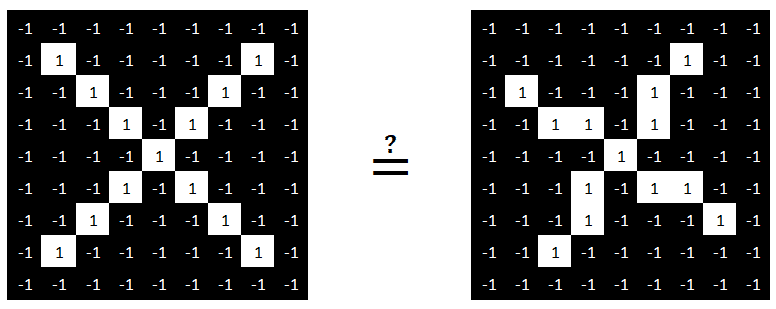
En comparant pixel par pixel¸ nous voyons qu’il y a des pixels différents entre les 2 images.

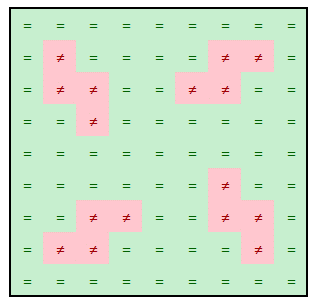
Pourtant, certains morceaux de l’image sont identiques entre les 2 images.

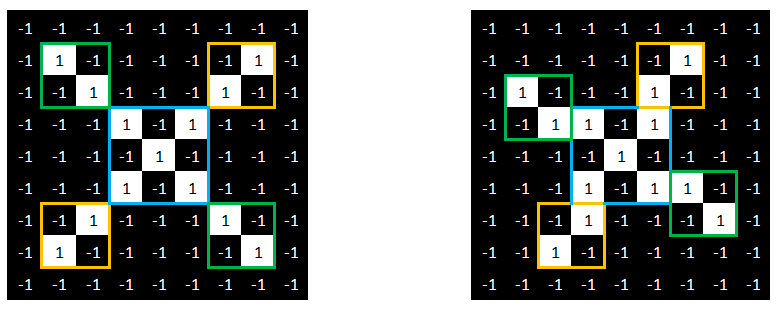
Ces morceaux sont au nombre de 3.

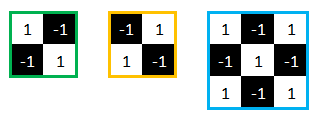
Nous appellerons désormais ces morceaux des features.

Considérons désormais des features de taille 3×3, nous allons voir comment la machine peut les trouver au moyen de calculs très simples.

Voici donc les nouvelles features que nous souhaitons que la machine trouve.

Nous allons commencer par rechercher cette feature sur cette image.

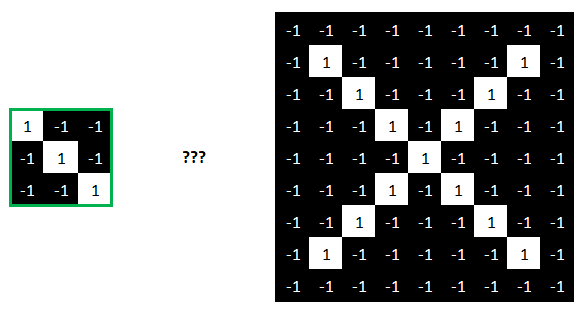
Pour cela, nous allons comparer cette feature en la faisant « glisser » sur l’image comme suit :

Etc.

Concrètement, pour comparer cette feature avec une partie de l’image, nous allons :

• 1/ multiplier les 9 valeurs des pixels de la caractéristique avec les 9 valeurs des pixels du morceau de l’image à trouver,
• 2/ additionner ces 9 résultats
• 3/ diviser par le nombre de pixels (ici 9)
• 4/ conclure (si le résultat est égal à 1, alors la feature a été identifiée dans l’image)

Voici un exemple :

1/ Multiplions les 9 valeurs des pixels de la feature avec les 9 valeurs des pixels du morceau de l’image à trouver.

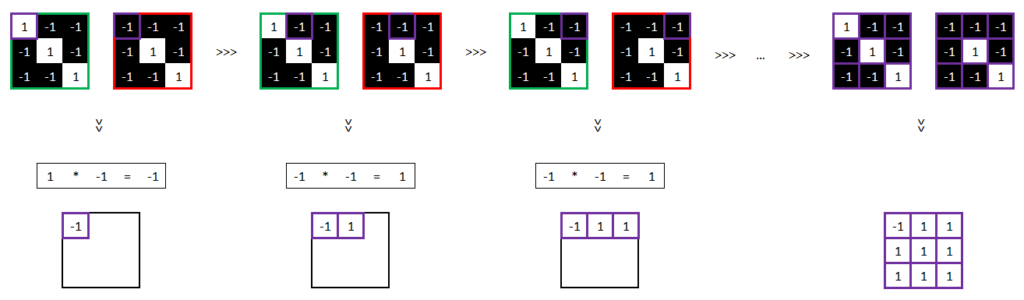
2/ Additionnons ces 9 résultats :

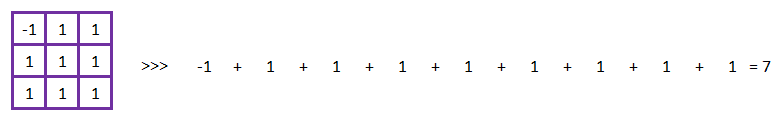
3/ Divisons par le nombre de pixels :

7 / 9 = 0,78

4/ Concluons :

0,78 est différent de 1, alors la caractéristique n’a pas été trouvée dans cette partie de l’image.

Nous pouvons refaire ces calculs pour le reste de l’image.

…

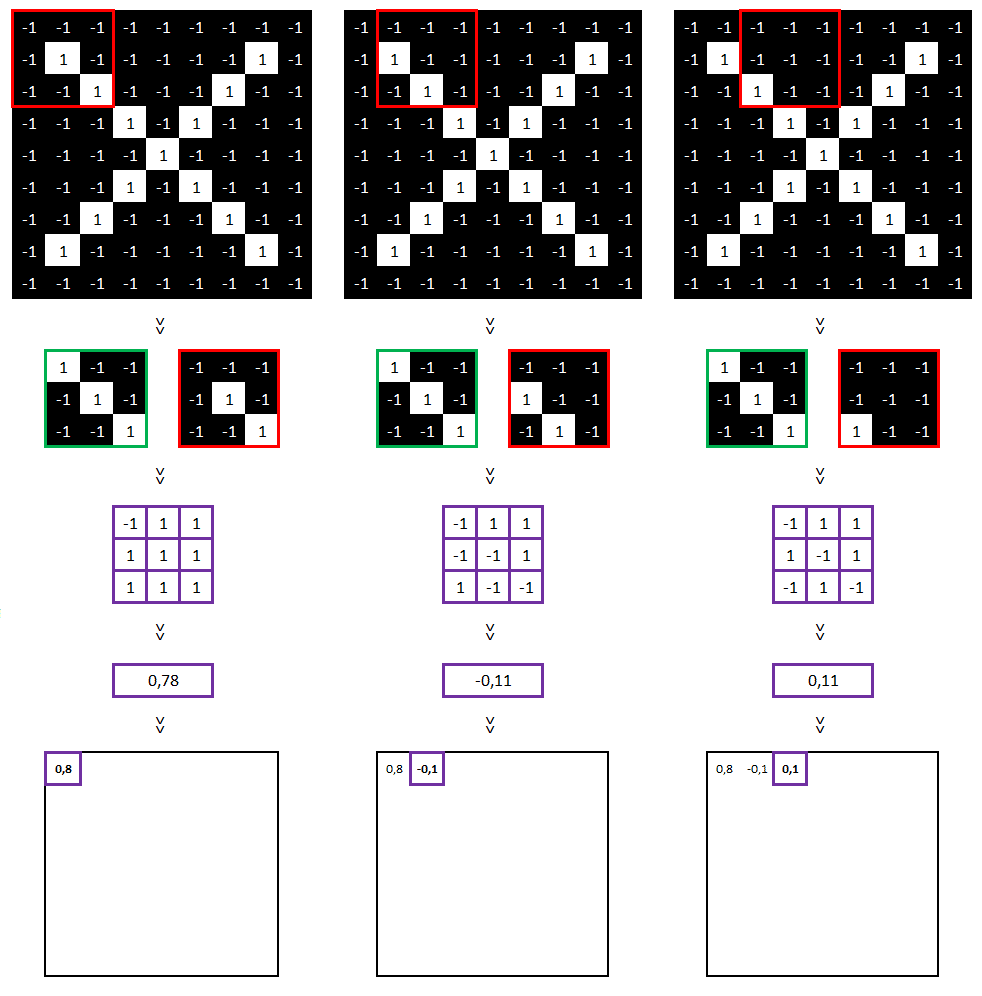
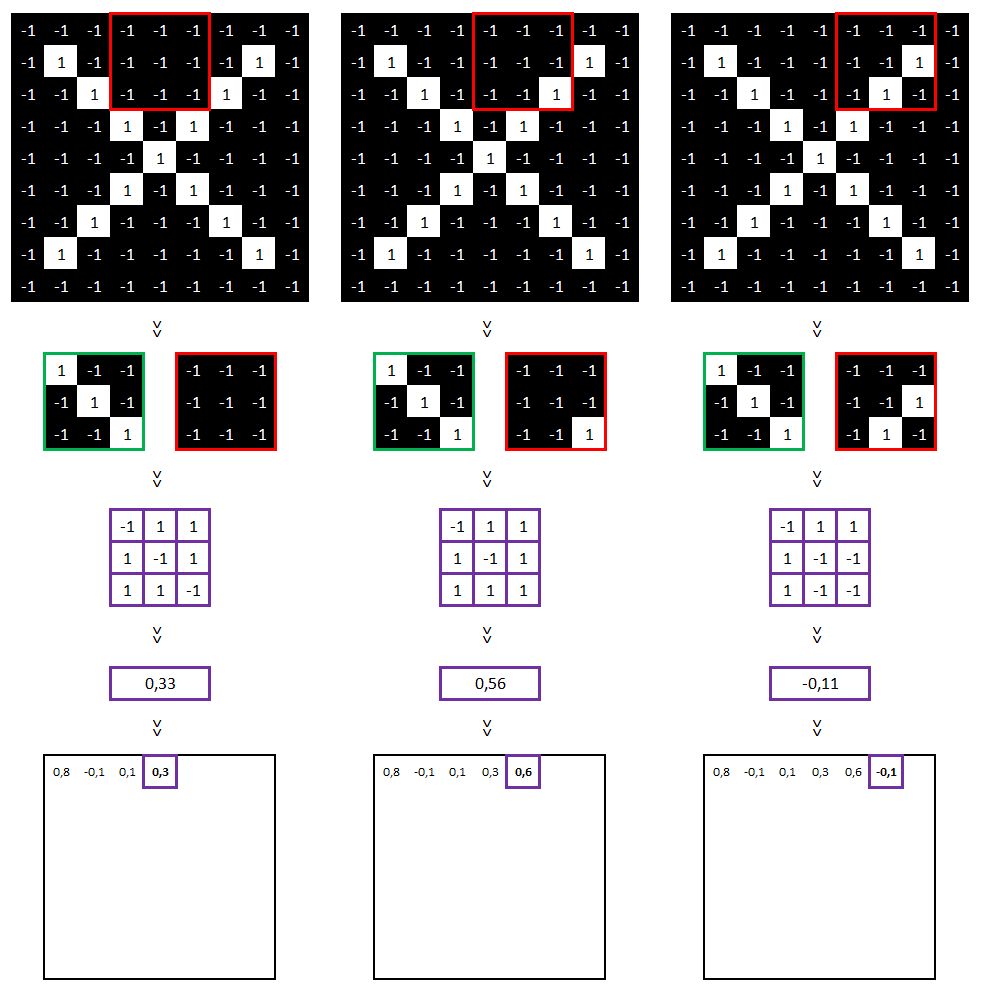
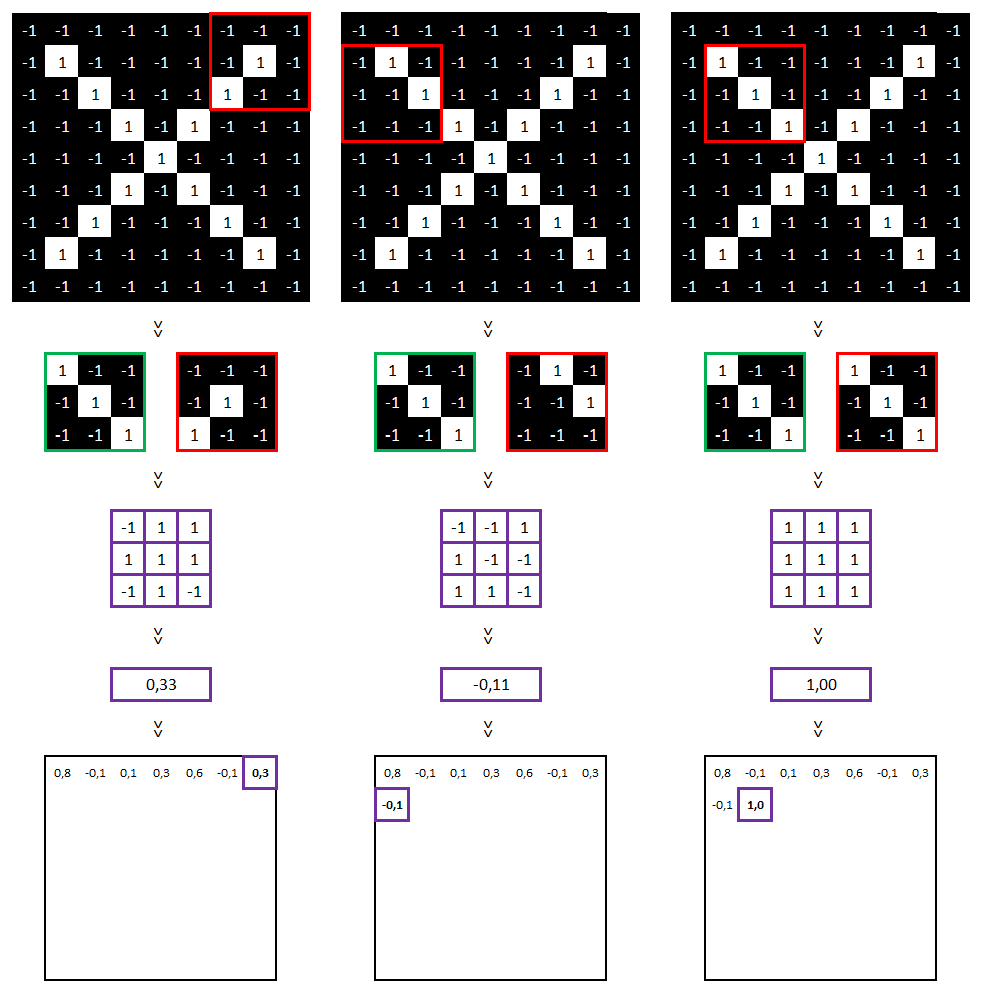
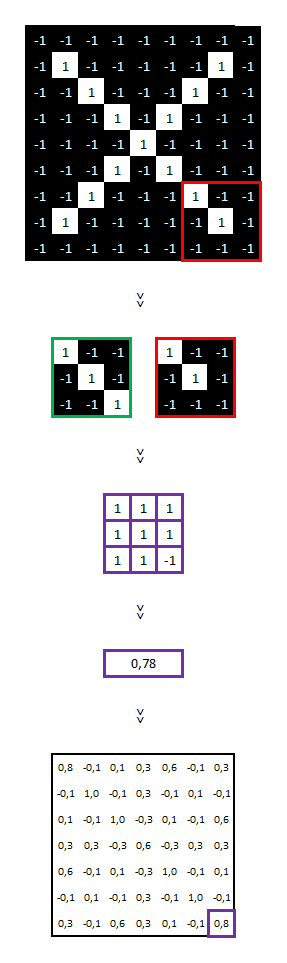
Pour information, voici les paramètres utilisés pour réaliser cette convolution : taille = 3×3, stride = 1 (i.e. la zone comparée bouge d’un seul pixel entre chaque comparaison).

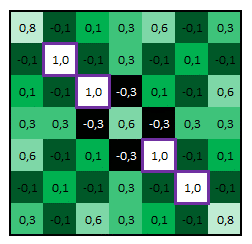
Sur cette nouvelle matrice, on y voit nos features « diagonales haut gauche vers bas droit » (les cellules égales à 1, entourées de violet ci-dessus). Ce qui est tout à fait cohérent au regard de notre image initiale.

Cette méthode fonctionne également si l’on inverse les couleurs (le résultat sera seulement égal à -1 et non à 1).

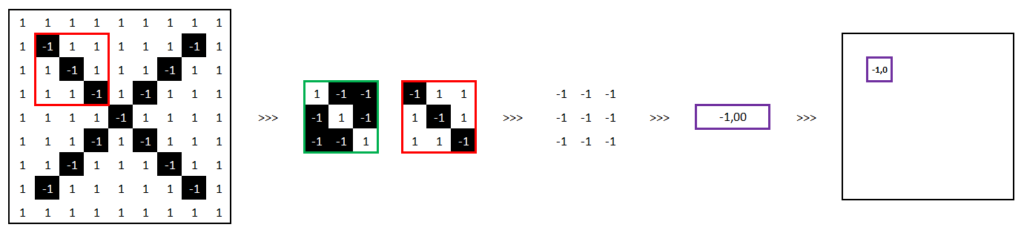
Ce que nous avons fait s’appelle une « convolution ».

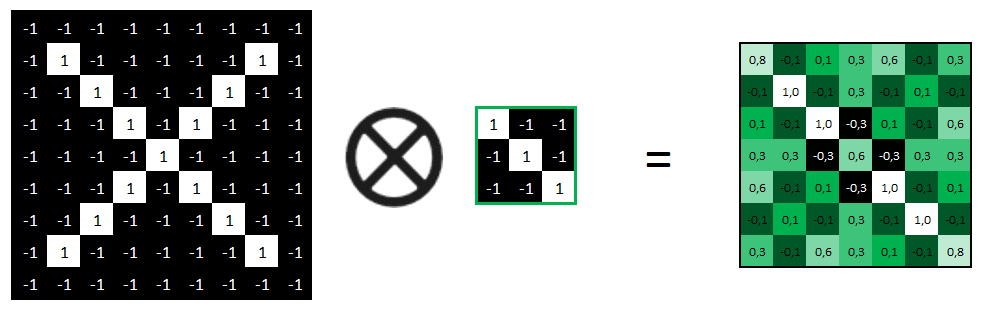
En refaisant ce même travail avec 2 autres features, nous obtenons 3 convolutions que l’on peut schématiser de la manière suivante.

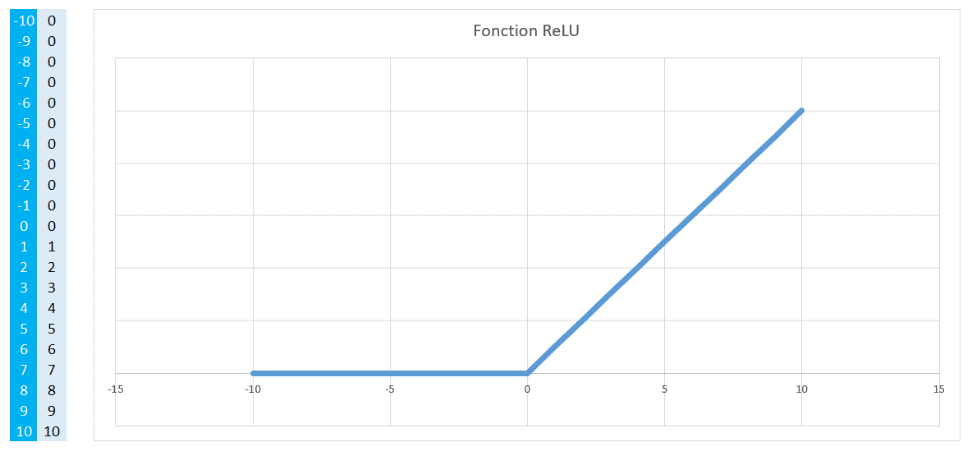
La fonction ReLU (Unité de rectification linéaire)

La fonction ReLU permet tout simplement :                     

• de transformer en 0 toutes les valeurs négatives
• de conserver les valeurs positives

Voici un exemple.

Appliquée à nos 3 matrices précédemment calculées, voici ce que ça donne.

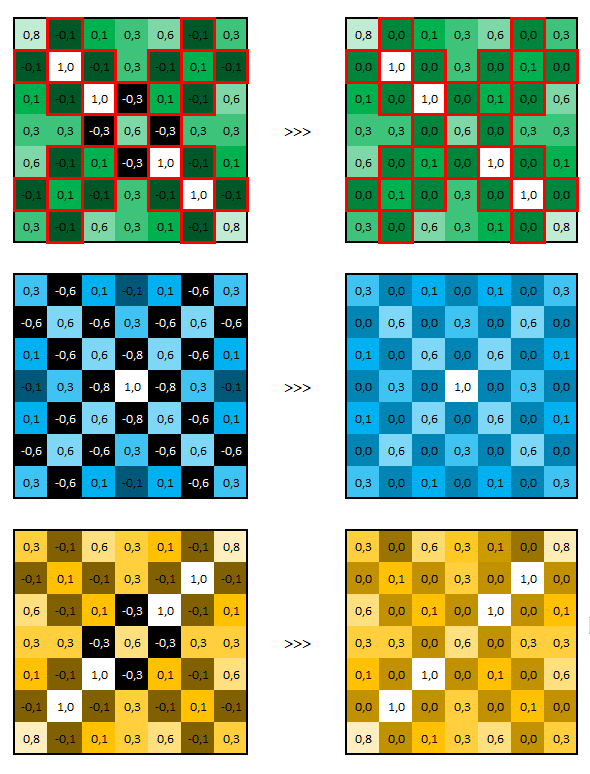
  Nous pouvons schématiser cette action ReLU de la manière suivante.

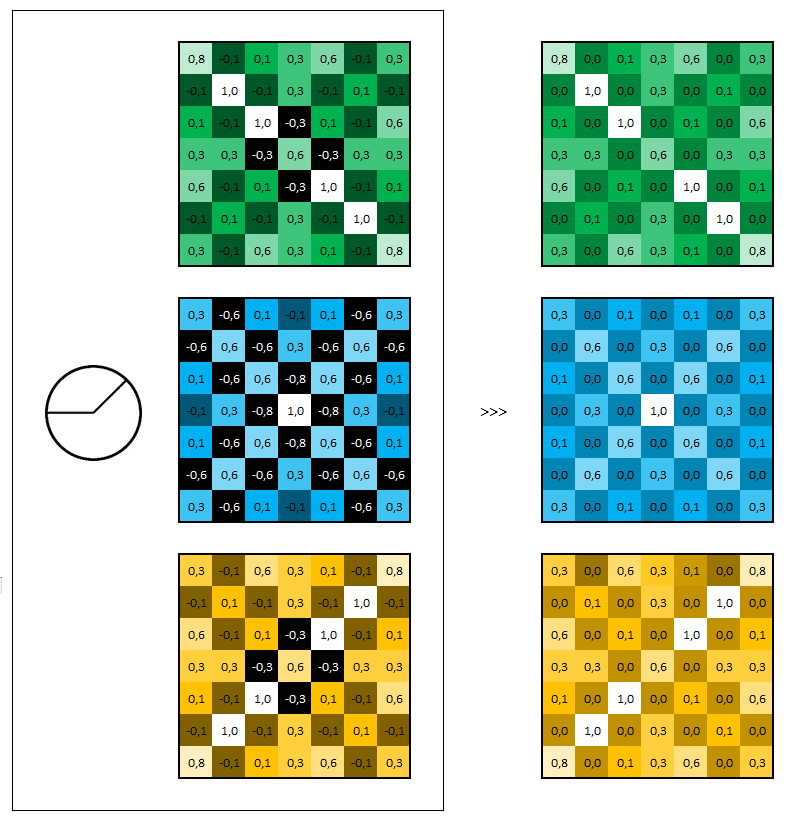
Le pooling

2 techniques existent, le max-pooling ou le mean-pooling. Généralement, c’est le max-pooling qui est choisi.

Le max-pooling prend la valeur maximale de chaque « morceau de l’image ».

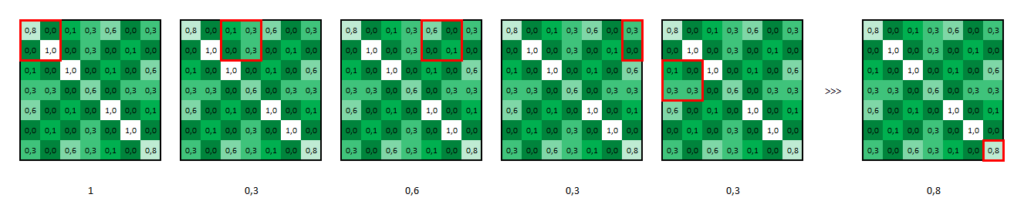
Appliquée à nos matrices précédemment calculées, voici ce que ça donne.

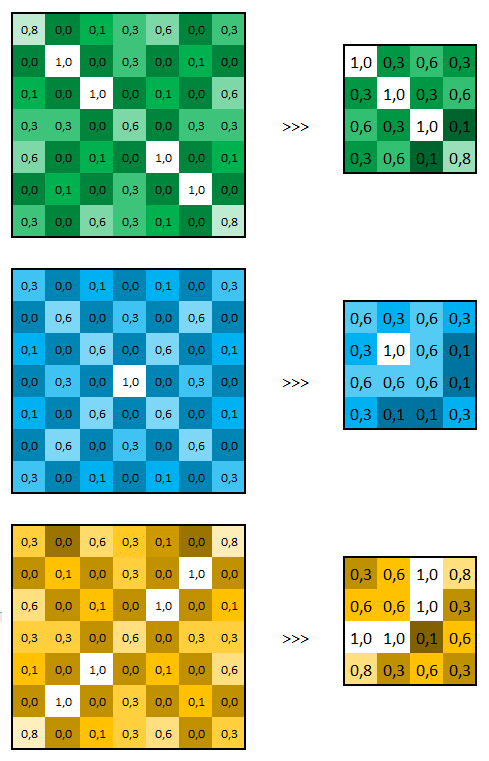
Pour information, les paramètres utilisés sont :
taille = 2×2, stripe = 1, valeurs des cellules absentes = 0.

Nous pouvons représenter ces actions de la manière suivante.

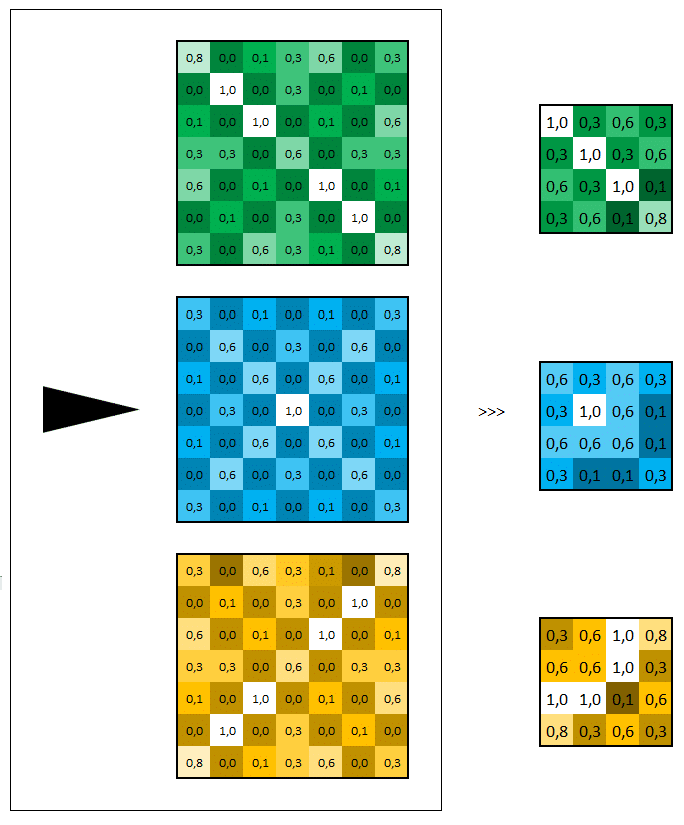
Le flattening (mise à plat)

Cela consiste tout simplement à prendre la totalité des valeurs de nos matrices précédemment calculées, et à les empiler, en vue de les exploiter dans la couche d’entrée d’un réseau de neurones.

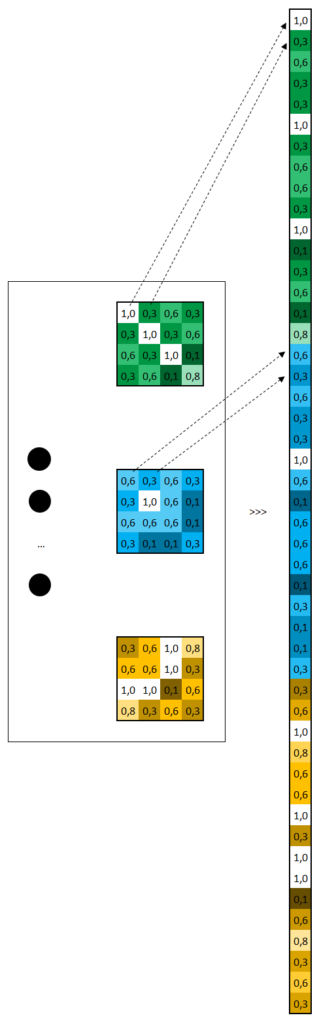
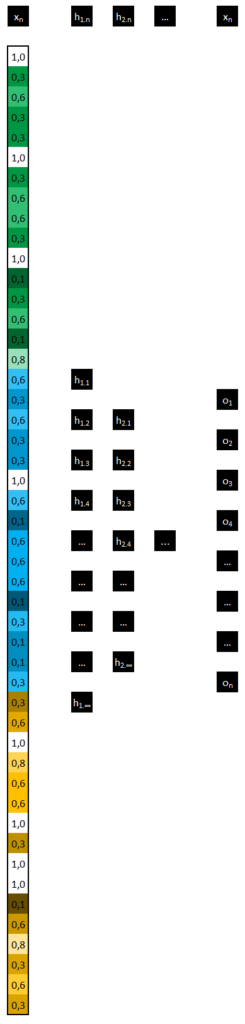
Le réseau de neurones fully connected

Comme notre réseau de neurones présenté précédemment, nous utilisons dans la couche d’entrée les valeurs calculées précédemment, nous ajoutons ensuite de 1 à une infinité de couches cachées à notre réseau, enfin, nous ajoutons en couche de sortie le nombre de neurones adéquats (ex. 2 neurones si nous souhaitons que notre réseau prédise la probabilité que l’image appartienne à la classe 1 ou à la classe 2).

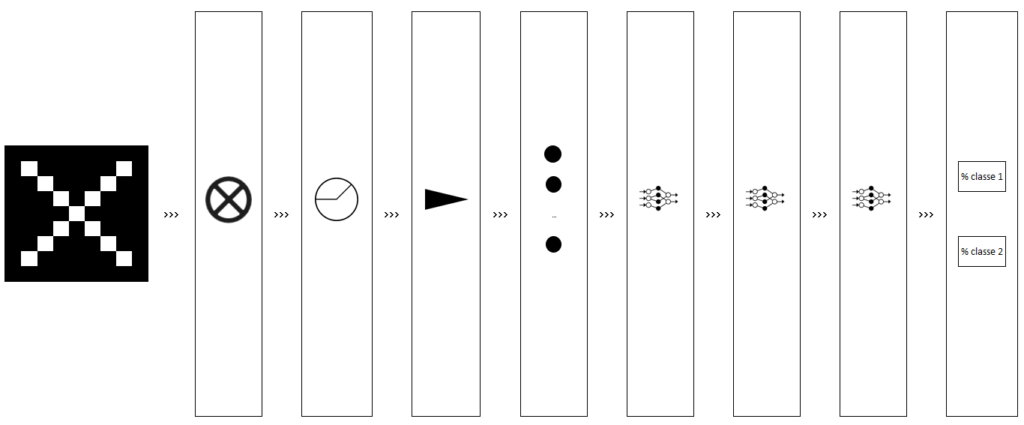
Synthèse

Voici une synthèse des actions précédemment décrites (rem : le réseau de neurones est constitué de 3 couches cachées, la couche de sortie est composée de 2 neurones).

Apprentissage d’un CNN

Notre dataset

Pour la suite de cet article, nous allons utiliser ces 2 images (respectivement une croix et un rond), mettre en place un CNN, puis l’entraîner afin qu’il minimise la fonction coût. Ce cas d’usage est pédagogique, dans la réalité, il n’aurait aucun intérêt à classer 2 images dont on connaît le label (càd ce qu’elles représentent).

Variables à ajuster

  Dans un CNN, 3 types de variables seront ajustés à chaque itération afin de minimiser notre fonction coût, à savoir :

• Les poids des couches du réseau de neurones fully connected
• Les biais des couches du réseau de neurones fully connected
• Les valeurs des pixels de notre filtre (exemple ci-dessous)

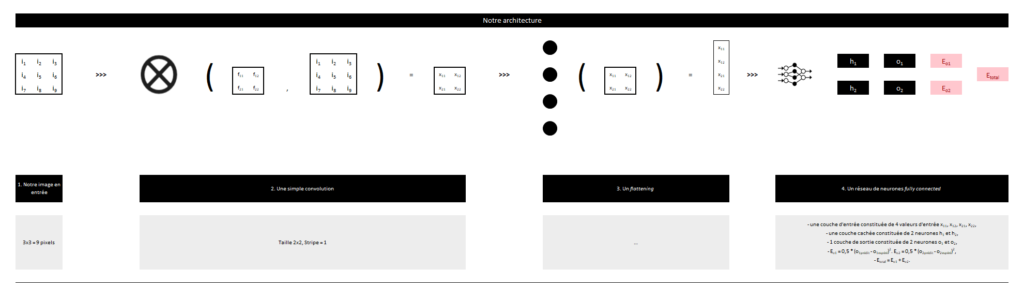
L’architecture de notre réseau

Si besoin, cliquer sur l’image pour l’agrandir :

A chacune des itérations, nous allons utiliser nos 2 images dans 2 réseaux identiques, partageant les mêmes poids, biais et valeurs pour le filtre et les neurones artificiels, seules les données d’entrées seront bien entendu différentes (ie. la valeur des pixels étant différentes entre les 2 images).

Voici ce que ela donne (si besoin, cliquer sur l’image pour l’agrandir).

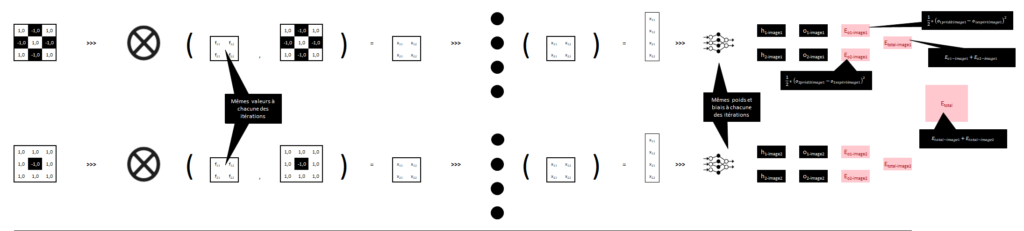
Objectif

Notre objectif est le suivant, entraîner le réseau jusqu’à ce que les 2 images soient correctement classées et donc :

E_total soit le plus proche possible de 0

donc

E_total-image1 et E_total-image2 soient également le plus proche possible de 0

donc

o_1-image1 soit le plus proche possible de 1
o_2-image1 soit le plus proche possible de 0
o_1-image2 soit le plus proche possible de 0
o_2-image2 soit le plus proche possible de 1

Rappelez-vous, l’image 1 appartient à la classe 1, et l’image 2 à la classe 2. (Si besoin, cliquer sur l’image pour l’agrandir)

Comme pour nos précédents réseaux de neurones, nous allons utiliser la méthode de la descente de gradient afin d’optimiser nos différentes variables :

Pour cela, comme expliqué également dans nos précédents articles, il va falloir trouver les formules de ∂E_total par rapport à chacune de ces 24 variables.

Certaines formules ont déjà été expliquées dans ces mêmes précédents articles, à savoir :

Si besoin, nous vous invitons à consulter notre article dédié à la mise en place de l’apprentissage d’un réseau de neurones.

Il nous manque donc les formules des dérivées suivantes :

Rappel Théorème de dérivation des fonctions composées

Nous vous avons déjà présenté le théorème de dérivation des fonctions composées, on sait donc que :

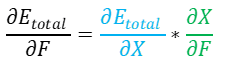
∂X / ∂F

Intéressons-nous dans un premier temps à ∂X / ∂F.

Pour rappel, voici les calculs effectués durant la convolution :

x₁₁ = i₁₁*f₁₁ + i₁₂*f₁₂ + i₂₁*f₂₁ + i₂₂*f₂₂
x₁₂ = i₁₂*f₁₁ + i₁₃*f₁₂ + i₂₂*f₂₁ + i₂₃*f₂₂
x₂₁ = i₂₁*f₁₁ + i₂₂*f₁₂ + i₃₁*f₂₁ + i₃₂*f₂₂
x₂₂ = i₂₂*f₁₁ + i₂₃*f₁₂ + i₃₂*f₂₁ + i₃₃*f₂₂

Développons nos différentes dérivées (∂X / ∂F).

(E_total / ∂X) * (∂X / ∂F)

Intéressons-nous désormais à (∂E_total / ∂X) * (∂X / ∂F).

X et F sont 2 matrices, les règles de dérivations matricielles nous permettent d’utiliser la formule suivante.

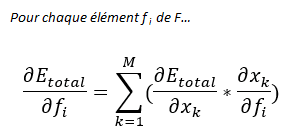
Nous avons ici 4 f (f₁₁, f₁₂, f₂₁, f₂₂), nous aurons donc 4 formules.

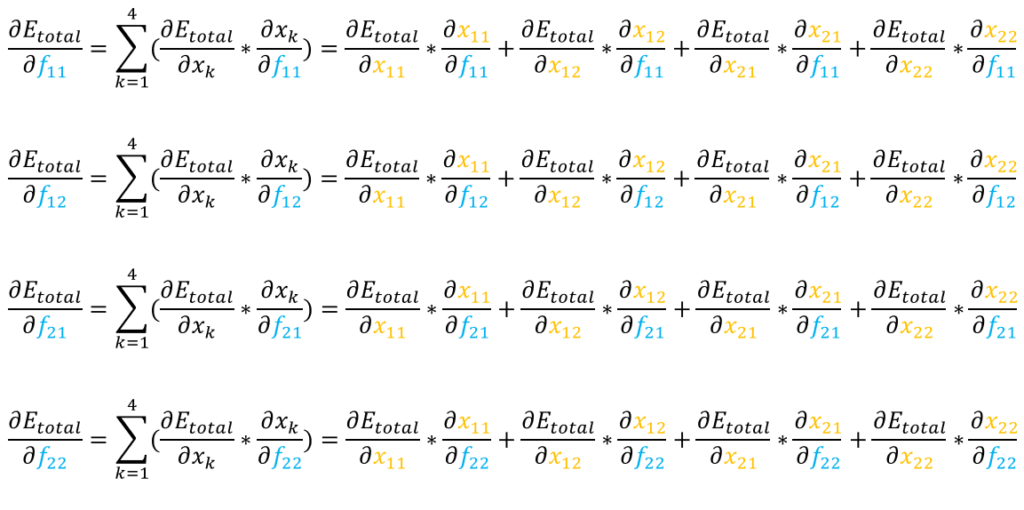
En utilisant les dérivées calculées précédemment, nous obtenons les formules suivantes.

Représentation visuelle de ∂Etotal / ∂F

• les 4 formules ont toutes la même « forme » (a*x + b*y + c*z + d*w),
• les 4 formules font toutes appel aux mêmes éléments (∂E_total / ∂x₁₁, ∂_Etotal / ∂x₁₂, ∂_Etotal / ∂x₂₁, ∂E_total / ∂x₂₂),
• la totalité des valeurs i des pixels de notre image en entrée sont utilisées (i₁₁, i₁₂, i₁₃, i₂₁, i₂₂, i₂₃, i₃₁, i₃₂, i₃₃).

Cela ressemble à une convolution.

Pour rappel, voici notre convolution initiale :

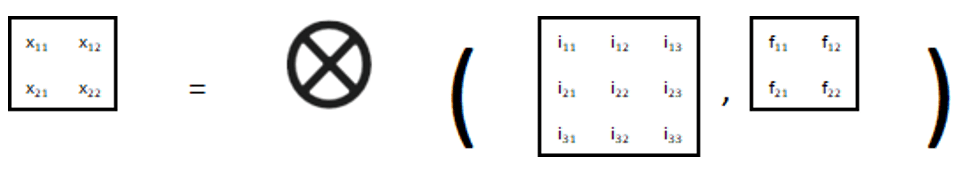
Exemple : x₁₁ = i₁₁ * f₁₁ + i₁₂ * f₁₂ + i₂₁ * f₂₁ + i₂₂ * f₂₂

Voici la convolution permettant d’obtenir les formules mathématiques des dérivées « ∂E_total / ∂F ».

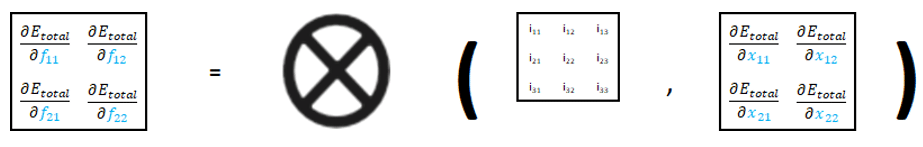
Nous vous invitons à vérifier par vous-même cette convolution, vous obtiendrez les mêmes résultats qu’indiqués précédemment.

∂E_total / ∂X

Il ne nous reste désormais plus qu’à trouver les formules « ∂E_total / ∂X ». 

En prenant par exemple x₁₁, et en faisant appel au théorème de dérivations des fonctions composées, ∂E_total / ∂x₁₁

Nous pouvons ainsi de la même manière trouver les formules des autres dérivées ∂E_total / ∂X, à savoir :

• ∂E_total / ∂x₁₂
• ∂E_total / ∂x₂₁
• ∂E_total / ∂x₂₂

Au travers de cet article, nous vous avons présenté les réseaux neuronaux convolutifs. Nous vous avons présenté les principales opérations utilisées dans ce type de réseau, puis vous avez pu voir comment il apprenait à corriger ses erreurs de prédiction. Vous pouvez trouver ici un fichier exploitant ces éléments afin de construire un modeste CNN.

👉 Retrouvez toute notre actu en temps réel en nous suivant sur LinkedIn 👈